To resume training of the model, the doc says I can specify the trace keyword of pm.sample.
Every time when I resume training of the model, the model seems to reinitialize the parameters.
Setting start=old_trace[-1] somehow make the sampling worse. While start=old_trace[-1] is the default, NUTS would override this default.
1st run:
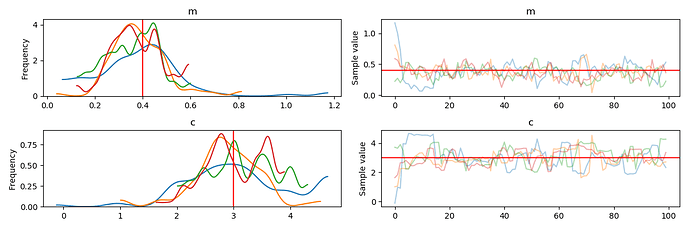
Combined trace of all runs of the sampler
I guess the spikes in the two subplots at the right means my code reinitialize the variables whenever it tries to resume training …
import theano.tensor as tt
import numpy as np
import pymc3 as pm
import matplotlib.pyplot as plt
import warnings
def gradients(vals, func, releps=1e-3, abseps=None, mineps=1e-9, reltol=1e-3,
epsscale=0.5):
"""
Calculate the partial derivatives of a function at a set of values. The
derivatives are calculated using the central difference, using an
iterative method to check that the values converge as step size decreases.
Parameters
----------
vals: array_like
A set of values, that are passed to a function, at which to calculate
the gradient of that function
func:
A function that takes in an array of values.
releps: float, array_like, 1e-3
The initial relative step size for calculating the derivative.
abseps: float, array_like, None
The initial absolute step size for calculating the derivative.
This overrides `releps` if set.
`releps` is set then that is used.
mineps: float, 1e-9
The minimum relative step size at which to stop iterations if no
convergence is achieved.
epsscale: float, 0.5
The factor by which releps if scaled in each iteration.
Returns
-------
grads: array_like
An array of gradients for each non-fixed value.
"""
grads = np.zeros(len(vals))
# maximum number of times the gradient can change sign
flipflopmax = 10.
# set steps
if abseps is None:
if isinstance(releps, float):
eps = np.abs(vals) * releps
eps[eps == 0.] = releps # if any values are zero set eps to releps
teps = releps * np.ones(len(vals))
elif isinstance(releps, (list, np.ndarray)):
if len(releps) != len(vals):
raise ValueError("Problem with input relative step sizes")
eps = np.multiply(np.abs(vals), releps)
eps[eps == 0.] = np.array(releps)[eps == 0.]
teps = releps
else:
raise RuntimeError(
"Relative step sizes are not a recognised type!")
else:
if isinstance(abseps, float):
eps = abseps * np.ones(len(vals))
elif isinstance(abseps, (list, np.ndarray)):
if len(abseps) != len(vals):
raise ValueError("Problem with input absolute step sizes")
eps = np.array(abseps)
else:
raise RuntimeError(
"Absolute step sizes are not a recognised type!")
teps = eps
# for each value in vals calculate the gradient
count = 0
for i in range(len(vals)):
# initial parameter diffs
leps = eps[i]
cureps = teps[i]
flipflop = 0
# get central finite difference
fvals = np.copy(vals)
bvals = np.copy(vals)
# central difference
fvals[i] += 0.5 * leps # change forwards distance to half eps
bvals[i] -= 0.5 * leps # change backwards distance to half eps
cdiff = (func(fvals) - func(bvals)) / leps
while 1:
fvals[i] -= 0.5 * leps # remove old step
bvals[i] += 0.5 * leps
# change the difference by a factor of two
cureps *= epsscale
if cureps < mineps or flipflop > flipflopmax:
# if no convergence set flat derivative
# (TODO: check if there is a better thing to do instead)
warnings.warn(
"Derivative calculation did not converge: setting "
"flat derivative.")
grads[count] = 0.
break
leps *= epsscale
# central difference
fvals[i] += 0.5 * leps # change forwards distance to half eps
bvals[i] -= 0.5 * leps # change backwards distance to half eps
cdiffnew = (func(fvals) - func(bvals)) / leps
if cdiffnew == cdiff:
grads[count] = cdiff
break
# check whether previous diff and current diff are the same within
# reltol
rat = (cdiff / cdiffnew)
if np.isfinite(rat) and rat > 0.:
# gradient has not changed sign
if np.abs(1. - rat) < reltol:
grads[count] = cdiffnew
break
else:
cdiff = cdiffnew
continue
else:
cdiff = cdiffnew
flipflop += 1
continue
count += 1
return grads
# define a theano Op for our likelihood function
class LogLikeWithGrad(tt.Op):
itypes = [tt.dvector] # expects a vector of parameter values when called
otypes = [tt.dscalar] # outputs a single scalar value (the log likelihood)
def __init__(self, loglike, data, x, sigma):
"""
Initialise with various things that the function requires. Below
are the things that are needed in this particular example.
Parameters
----------
loglike:
The log-likelihood (or whatever) function we've defined
data:
The "observed" data that our log-likelihood function takes in
x:
The dependent variable (aka 'x') that our model requires
sigma:
The noise standard deviation that out function requires.
"""
# add inputs as class attributes
self.likelihood = loglike
self.data = data
self.x = x
self.sigma = sigma
# initialise the gradient Op (below)
self.logpgrad = LogLikeGrad(self.likelihood, self.data, self.x,
self.sigma)
def perform(self, node, inputs, outputs):
# the method that is used when calling the Op
theta, = inputs # this will contain my variables
# call the log-likelihood function
logl = self.likelihood(theta, self.x, self.data, self.sigma)
outputs[0][0] = np.array(logl) # output the log-likelihood
def grad(self, inputs, g):
# the method that calculates the gradients - it actually returns the
# vector-Jacobian product - g[0] is a vector of parameter values
theta, = inputs # our parameters
return [g[0] * self.logpgrad(theta)]
class LogLikeGrad(tt.Op):
"""
This Op will be called with a vector of values and also return a vector of
values - the gradients in each dimension.
"""
itypes = [tt.dvector]
otypes = [tt.dvector]
def __init__(self, loglike, data, x, sigma):
"""
Initialise with various things that the function requires. Below
are the things that are needed in this particular example.
Parameters
----------
loglike:
The log-likelihood (or whatever) function we've defined
data:
The "observed" data that our log-likelihood function takes in
x:
The dependent variable (aka 'x') that our model requires
sigma:
The noise standard deviation that out function requires.
"""
# add inputs as class attributes
self.likelihood = loglike
self.data = data
self.x = x
self.sigma = sigma
def perform(self, node, inputs, outputs):
theta, = inputs
# define version of likelihood function to pass to derivative function
def lnlike(values):
return self.likelihood(values, self.x, self.data, self.sigma)
# calculate gradients
grads = gradients(theta, lnlike)
outputs[0][0] = grads
def my_model(thetha, x):
m, c = thetha
return m * x + c
def my_loglike(theta, x, data, sigma):
"""
A Gaussian log-likelihood function for a model with parameters given in theta
"""
model = my_model(theta, x)
return -(0.5 / sigma ** 2) * np.sum((data - model) ** 2)
def main():
# set up our data
N = 10 # number of data points
sigma = 1. # standard deviation of noise
x = np.linspace(0., 9., N)
mtrue = 0.4 # true gradient
ctrue = 3. # true y-intercept
truemodel = my_model([mtrue, ctrue], x)
# make data
np.random.seed(
716742) # set random seed, so the data is reproducible each time
data = sigma * np.random.randn(N) + truemodel
ndraws = 100 # number of draws from the distribution
nburn = 10 # number of "burn-in points" (which we'll discard)
# create our Op
logl = LogLikeWithGrad(my_loglike, data, x, sigma)
# use PyMC3 to sampler from log-likelihood
with pm.Model() as opmodel:
m = pm.Uniform('m', lower=-10., upper=10.)
c = pm.Uniform('c', lower=-10., upper=10.)
theta = tt.as_tensor_variable([m, c])
pm.DensityDist('likelihood', lambda v: logl(v),
observed={'v': theta})
trace = pm.sample(ndraws, tune=nburn,
discard_tuned_samples=True)
_ = pm.traceplot(trace, lines={'m': mtrue, 'c': ctrue})
plt.show()
for i in range(5):
trace = pm.sample(ndraws, tune=nburn,
discard_tuned_samples=True, trace=trace,
start=None)
print("trace_len", len(trace)) # trace is the combined trace from all 5 runs.
# plot the traces
_ = pm.traceplot(trace, lines={'m': mtrue, 'c': ctrue})
# put the chains in an array (for later!)
samples_pymc3_2 = np.vstack((trace['m'], trace['c'])).T
plt.show()
main()