@ferrine
The model is working correctly for me as described before, (without change to symbolic_random).
Now the only thing I’m working on is getting Minibatch to work.
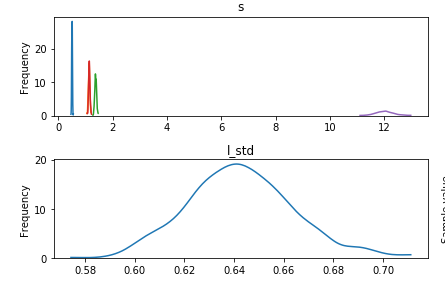
Here are the weights traceplot from the full dataset

While the weights from the Minibatch dataset are very similar, their sds are higher, and the cov parameter is underestimated. (the resulting correlation matrix is almost all 0)

To clarify, here’s the code I’m working with:
class NormalMixture(pm.Mixture):
def __init__(self, w, mu, comp_shape=(), *args, **kwargs):
sd=kwargs.pop('sd',None)
self.mu = mu = tt.as_tensor_variable(mu)
self.sd = sd = tt.as_tensor_variable(sd)
super(NormalMixture, self).__init__(w, [pm.Normal.dist(mu[0], sd=sd[0]),pm.Normal.dist(mu[1], sd=sd[1])],
*args, **kwargs)
def _repr_latex_(self, name=None, dist=None):
if dist is None:
dist = self
mu = dist.mu
w = dist.w
sd = dist.sd
name = r'\text{%s}' % name
return r'${} \sim \text{{NormalMixture}}(\mathit{{w}}={},~\mathit{{mu}}={},~\mathit{{sigma}}={})$'.format(name,
get_variable_name(w),
get_variable_name(mu),
get_variable_name(sd))
@Group.register
class SymmetricMeanFieldGroup(MeanFieldGroup):
"""Symmetric MeanField Group for Symmetrized VI"""
__param_spec__ = dict(smu=('d', ), rho=('d', ))
short_name = 'sym_mean_field'
alias_names = frozenset(['smf'])
@node_property
def mean(self):
return self.params_dict['smu']
def create_shared_params(self, start=None):
if start is None:
start = self.model.test_point
else:
start_ = start.copy()
update_start_vals(start_, self.model.test_point, self.model)
start = start_
if self.batched:
start = start[self.group[0].name][0]
else:
start = self.bij.map(start)
rho = np.zeros((self.ddim,))
if self.batched:
start = np.tile(start, (self.bdim, 1))
rho = np.tile(rho, (self.bdim, 1))
return {'smu': theano.shared(
pm.floatX(start), 'smu'),
'rho': theano.shared(
pm.floatX(rho), 'rho')}
#@node_property
#def symbolic_random(self):
# initial = self.symbolic_initial
# sigma = self.std
# mu = self.mean
# sign = theano.tensor.as_tensor([-1, 1])[self._rng.binomial(sigma.ones_like().shape)]
#
# return sigma * initial + mu * sign
@node_property
def symbolic_logq_not_scaled(self):
z = self.symbolic_random
mu=theano.tensor.stack([self.mean, -self.mean])
sd=theano.tensor.stack([self.std, self.std])
logq = NormalMixture.dist(w=theano.tensor.stack([.5,.5]),
mu=mu,
sd=sd
).logp(z)
return logq.sum(range(1, logq.ndim))