A bug with Binomial on non-scalar arguments?

Questions
1

Consider the following, simple model:

import pymc3 as pm 
import numpy as np

with pm.Model() as model:
    pm.Binomial('scalar_binomial', n=1, p=0.25)
    pm.Binomial('arrayed_binomial', n=1, p=0.25, shape=10)
    pm.Binomial(
        'arrayed_binomial_alt', n=np.ones(10), 
        p=np.full(10, 0.25), shape=10)
    
    trace = pm.sample(draws=600, chains=2, tune=500)
    summary = pm.summary(
        trace, 
        var_names=[
            'scalar_binomial', 'arrayed_binomial', 
            'arrayed_binomial_alt'])
summary

The three RVs are identical binomials, except that the first scalar_binomial
is a scalar, the second arrayed_binomial has shape 10 with scalar arguments,
and the third arrayed_binomial_alt has shape 10 with (identical) arrayed
arguments. Note also that nothing in this model is constrained by observations.

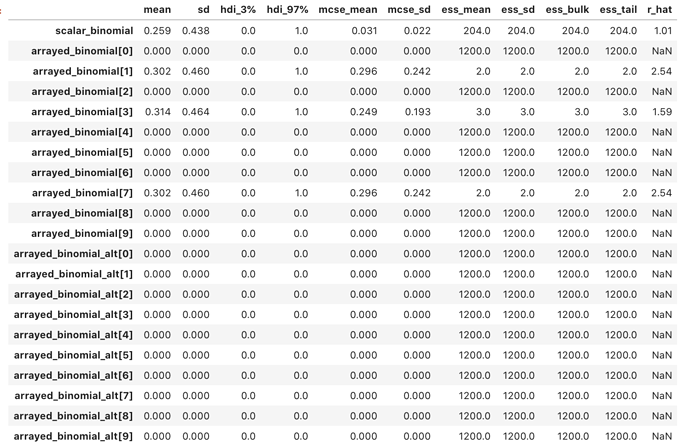
The result of sampling is peculiar:

image
image1498×970 76.6 KB

scalar_binomial is as expected. arrayed_binomial sees 7 of the 10 array
elements with no binomial samples, and means of 0.0. arrayed_binomial_alt
sees all 10 array elements with no binomial samples, and means of 0.0.

Is this a bug with pm.Binomial()? But how could a bug on something this basic escape notice? So perhaps I am misunderstanding.

The same model structure with normals instead of binomials produces expected
results:

import pymc3 as pm 
import numpy as np

with pm.Model() as model:
    pm.Normal('scalar_normal', mu=1, sigma=0.25)
    pm.Normal('arrayed_normal', mu=1, sigma=0.25, shape=10)
    pm.Normal(
        'arrayed_normal_alt', mu=np.ones(10), 
        sigma=np.full(10, 0.25), shape=10)
    
    trace = pm.sample(
        draws=600, chains=2, tune=500, 
        step=pm.Metropolis())   # Metropolis so the sampling is identical to above
    summary = pm.summary(
        trace, 
        var_names=[
            'scalar_normal', 'arrayed_normal', 'arrayed_normal_alt'])
summary

Results, as expected:

image
image1488×974 102 KB

Configuration:
PyMC3 v3.9.3
Numpy v1.19.4
Theano v1.0.5

2

@aseyboldt, @junpenglao, @lucianopaz is this a bug? Or is this expected behavior?

3

@ckrapu explained the issue elsewhere:

Perhaps somewhat surprisingly, this is not a bug and is expected behavior for MCMC using the Metropolis proposal. The short version of this explanation is that all the proposals for the vector version are getting rejected.

The longer explanation is this: for arrayed_binomial has its starting value in the distribution’s mode. Hence, any proposal which flips any of the zeros to ones will lead to a lower likelihood and thus is relatively unlikely. I suspect that you may need 10k+ Metropolis proposals to get a few successful samples here. If you change the probability from 0.25 to 0.5 you will see that new samples will be drawn successfully and there will be meaningful sampler statistics. This effect is most pronounced when the proposal is multidimensional. Hence, the scalar case is unaffected by this issue.

I think this shortcoming of Metropolis means that neither sample_posterior_predictive() nor fast_sample_posterior_predictive() can be used on a model that includes an array of binomials.

4

One approach to this problem is to create a model factory (hat tip: @lucianopaz) that creates pymc3 binomials for the initial MCMC inference, and deterministics with theano binomials for the posterior predictive inference. I am assuming the latter can be simulated.

5

@bridgeland, thanks for bringing this up. The forward sampling algorithms will work fine, the problem is the trace.
What this issue highlights is that making proposals in MCMC from discrete variables is hard, and making proposals for a batch of discrete variables is harder, as multiple changes can lead to worse overall logp, that end up always being rejected.
The real solution to this problem would be to come up with a better step method to use here. I can’t think of a general solution that would always work, but at least in this problem, it looks like running a Gibbs step for each element of the binomial RV should work.

1 Like
6

Thank you for your explanation Luciano. @lucianopaz

I think you are suggesting that one of the two Gibbs step methods be used for those troublesome binomial RVs, either BinaryGibbsMetropolis or CategoricalGibbsMetropolis. (Please correct me if I misunderstand.)

That may work in the simple example above, but my actual model is not so simple. In my more complex model the offending binomial RV takes a tensor for its n parameter—a tensor of shape=50—and n is only 1 for some of the tensor array, sometimes. Otherwise n is 2 or 10 or 20. So I think neither BinaryGibbsMetropolis nor CategoricalGibbsMetropolis will work.

Unless I misunderstand your suggestion, or misunderstand these two Gibbs step methods.

7

Regretably, neither of those step methods would work for you. I meant a Gibbs step method in a broader sense.
What Gibbs step means is that you want to sequentially make proposals that change a single entry in the binomial RV, accept our reject that proposal based on the resulting logp and then move on to the next entry. This means that you will be making proposals based on a marginal version of the models logp. If I understand correctly, pymc doesn’t have that out of the box but maybe @junpenglao or @michaelosthege can correct me if I’m wrong.
I’ll try to think of a way to help you with your particular problem. I’m not entirely sure if this would work, but maybe if instead of instantiating a single binomial RV with shape 50, you instantiated 50 scalar RVs, the metropolis step method would work sequentially through each scalar RV (a la Gibbs).

1 Like
8

Ugh.

What about a model factory approach? A model factory function could create a backwards version of the model, with a binomial tensor tied to an observation, and also a forwards version of the model, with a deterministic that uses a theano binomial to simulate:

if direction == 'backward':
    won = pm.binomial('won', n=foo, p=bar, observed=observed_won)
elif direction == 'forward':
    won = deterministic('won', self._rng.binomial(n=foo, p=bar))
else:
    raise Error(f'Bad direction: {direction}')

Then the approach you explained elsewhere could be employed:

with backward_model:
    df = pm.trace_to_dataframe(
        forward_trace, varnames=[...], include_transformed=True) 
    ppc = pm.sample_posterior_predictive(
        trace=df.to_dict('won'), samples=len(df))

Will this approach work?

9

Ah, yes! But this would only work if the binomial is observed when you run pm.sample. I was thinking of a situation in which your binomial was a latent parameter that had to be inferred

1 Like