Sorry if I wasn’t clear before and that I didn’t provide more concrete examples. My question was intended to ask for general guidelines rather than to solve a specific modelling issue. The main goal is to have analyses that can be implemented in a federated context. However, we may face several problems regarding data sharing restrictions or labs unable to implement our software/models. In that case, a meta-analytic approach where we can combine the estimates from each lab, would be very useful. In short, there’s no single solution to our problem (no single right direction), but hopefully many that can be implemented together and/or alternatively. So, all ideas related to this topic are welcome.
But to give you a more concrete idea, suppose I want to estimate incubation periods of a disease, the data are exposure start times and symptoms onset times, and the observed data to input in the model would be start - onset (here I represent that simply by sampling randomly from a Gamma distribution):
# -*- coding: utf-8 -*-
import pymc as pm
import arviz as az
import numpy as np
import pytensor.tensor as pt
#lab 1 estimate
N1 = 20
mu1 = 9
sig1 = 1
# exposure start minus symptoms onset
obs1 = np.random.gamma(shape=mu1, scale=sig1, size=N1).round(0)
with pm.Model() as mod1:
a = pm.Gamma("a", 1, 1)
b = pm.HalfNormal("b", 1, shape=N1)
m = pm.Deterministic("m", a + b)
s = pm.Gamma("s", 1, 1) #standard deviation parameter
y = pm.Gamma("y", mu=m, sigma=s, observed=obs1)
idata1 = pm.sample()
m1 = az.extract(idata1.posterior)['m'].values.mean(axis=1)
s1 = az.extract(idata1.posterior)['s'].values.mean()
az.plot_posterior(idata1, var_names=["mu"], hdi_prob=0.9)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [a, b, s]
|████████████| 100.00% [8000/8000 00:31<00:00 Sampling 4 chains, 0 divergences]Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 53 seconds.
#lab 2 estimate
N2 = 40
mu2 = 9
sig2 = 1
# exposure start minus symptoms onset
obs2 = np.random.gamma(shape=mu2, scale=sig2, size=N2).round(0)
with pm.Model() as mod2:
a = pm.Gamma("a", 1, 1)
b = pm.HalfNormal("b", 1, shape=N2)
m = pm.Deterministic("m", a + b)
s = pm.Gamma("s", 1, 1) #standard deviation parameter
y = pm.Gamma("y", mu=m, sigma=s, observed=obs2)
mu = pm.Deterministic("mu", m.mean())
idata2 = pm.sample()
m2 = az.extract(idata2.posterior)['m'].values.mean(axis=1)
s2 = az.extract(idata2.posterior)['s'].values.mean()
az.plot_posterior(idata2, var_names=["mu"], hdi_prob=0.9)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [a, b, s]
|████████████| 100.00% [8000/8000 00:33<00:00 Sampling 4 chains, 0 divergences]Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 55 seconds.
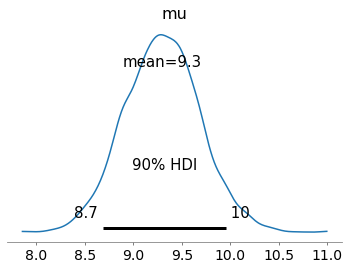
Now, supposing that lab1 and lab2 cannot share the observed data, what would be an appropriate metanalytic approach to combine the estimates from parameters m and s? As mentioned in my previous post (reference there), I attempted this:
## approach from Levenson et al (2000)
n = np.array([N1, N2])
x = np.array([m1.mean(), m2.mean()])
s = np.array([s1, s2])
with pm.Model() as mod:
t = pm.StudentT("t", mu=0, sigma=1, nu=n-1, shape=2)
m = pm.Deterministic("m", x + (s/pt.sqrt(n))*t)
l = m.sum()/len(x) - pt.abs(m.max()-m.min())/2
u = m.sum()/len(x) + pt.abs(m.max()-m.min())/2
sigma = pm.Deterministic("sigma", pt.abs(m.max()-m.min())/2)
mu = pm.Uniform("mu", lower=l, upper=u)
idata_a = pm.sample()
az.plot_posterior(idata_a, var_names=["mu"], hdi_prob=0.9)
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>Metropolis: [t]
>NUTS: [mu]
|████████████| 100.00% [8000/8000 00:24<00:00 Sampling 4 chains, 0 divergences]Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 46 seconds.
Which gave results not too different from a hierarchical model like this one:
## hierarchical model using estimates as observed
n = np.array([N1, N2])
x = np.concatenate([m1, m2])
s = np.array([s1, s2])
j = np.concatenate([np.repeat(0,N1), np.repeat(1,N2)])
with pm.Model() as mod:
ms = pm.HalfNormal("ms", sigma=1)
ml = pm.HalfNormal("ml", sigma=1)
m = pm.Gamma("m", mu=ml, sigma=ms, shape=len(n))
sigma = pm.HalfNormal("sigma", s.mean())
y = pm.Gamma("y", mu=m[j], sigma=sigma, observed=x)
mu = pm.Deterministic("mu", m.mean())
idata_b = pm.sample()
az.plot_posterior(idata_b, var_names=["mu"], hdi_prob=0.9)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [ms, ml, m, sigma]
|████████████| 100.00% [8000/8000 00:35<00:00 Sampling 4 chains, 0 divergences]Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 56 seconds.
Are these approaches appropriate? Are they outside the context/scope of a meta-analytic approach? Thanks.
It sounds like a cool problem. From all the thing mentioned in this thread I only really know about meta analysis. That approach could be useful if the data from each lab are basically summary statistics (sample size and some mean and spread parameters and or effect sizes). The specifics about how to deal with that does depend on the form of the data though. I don’t have any immediate “ah ha” about the solution though, but I’ll keep an eye on this thread as I’m interested in what route you take