Dear all,
I am currently working on a research project where I would like to apply what I have learned in this course into practice. Sorry in advance that this post is quite long because (1) applying the knowledge and skills into real-world data has brought me a lot of questions, and (2) I would like to provide information that is as detailed as I can so that you can help with navigating the problems. Thank you so much for your guidance!!
List of questions:
- Question 1: Interpretation based on correlation and scatterplot
- Question 2 - Outliers
- Questions 3.1 & 3.2 - All about priors
The context of the project:
- Outcome variable: the number of green technology patents at time period t+1
- Explanatory variable: the number of natural disasters at the time period t.
- Unit of analysis: Indian states across different time periods.
I would like to know whether there is any relationship between these two variables in Indian states. Put differently, the research question is whether having a lot of natural disasters during this time period would make the Indian states more likely to produce more green technology patents in the next time period?
The data frame looks like this:
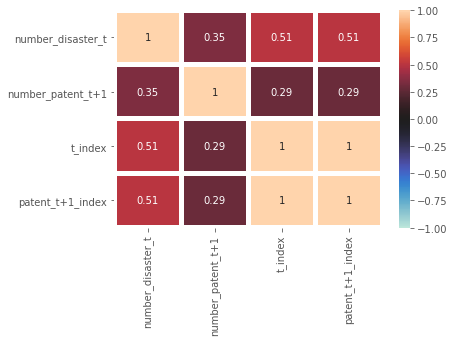
The correlation heat map looks like this:
The pairplot looks like this:
Question 1 - Interpretation based on correlation and scatterplot
Unlike the fish example that we have in the course, the scatterplot about the variables ‘number_disaster_t’ and ‘number_patent_t+1’ are not that linear. Instead, they are quite spread across the graph with no clear shapes. This might indicate that their correlation is not that strong and the relationship is not that linear. However, I have noticed that their correlation (shown in the correlation heat map) is 0.35. As a social scientist, I personally think that this is already very good because the correlation is above 0.25.
Thus, these pieces of information seem to be contradictory to me, and I am not sure how to interpret this. In addition, I am wondering whether I can still use a generalized linear regression to understand the relationship between these two variables?
Question 2 - Outliers
As green technology is somewhat new, there are not many patents in this field in the previous time periods (see the figure as the distribution of green technology patents by time period below).
In particular, if I zoom into the number of green technology patents that each state had, the variation is very big - some states had a lot of these patents (the most outstanding outlier had even around 30,000 patents in one period) while other states had very few of them.
Thus, my question here is whether I should remove those outliers shown in the following box plot?
Now questions about modelling:
I constructed a negative binomial regression model because (1) the number of patent is count data, and (2) the variance of the outcome variable is much larger than its mean (see the next figure):
The first version of my Bayesian negative binomial regression model (with very small priors) is shown as below:
COORDS = {
'slopes': ['number_disaster_t'],
}
with pm.Model(coords=COORDS) as green_tech_without_control:
# Data
number_disaster_t = pm.ConstantData('number_disaster_t',
df.number_disaster_t.values,)
# Prior
intercept = pm.Normal('intercept', mu=0, sigma=1)
β = pm.Normal('β', mu=0, sigma=1, dims=('slopes'))
alpha = pm.Exponential('alpha', 0.5)
# Linear regression
mu = pm.math.exp(
intercept
+ β[0] * number_disaster_t
)
# Likelihood, y_estimated
pm.NegativeBinomial(
'number_patent_t+1',
mu=mu,
alpha=alpha,
observed=df['number_patent_t+1'].values,
)