Bayesian Value at Risk

Questions
1

Hello !

Last week I started to ask myself how I could estimate Value at Risk of a financial security from a Bayesian approach. I started my research and I found that Pyfolio gave a first solution (in Bayesian tear-sheet) :

Bayesian VaR - Pyfolio.jpg1634×244 53.4 KB

As it is a fixed value and not a probability distribution, it is not exactly what I expected. As I understood it is the VaR estimated from simulated returns.

I made a small notebook to illustrate my intuition. I started by generating toy data :

data = sp.stats.t.rvs(8, loc = 0, scale = 0.4,  size = 504)

And my model is the following (helped by Pyfolio):

with pm.Model() as model2:
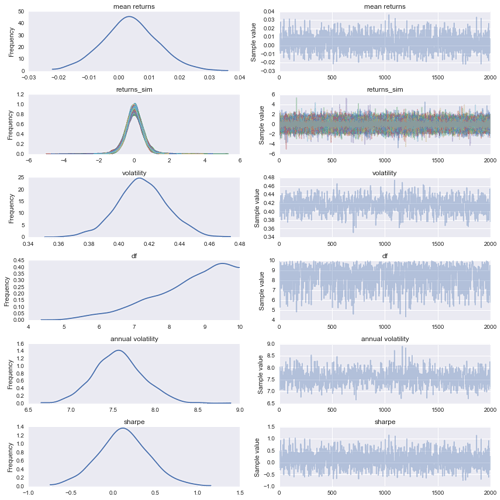
    mu = pm.Normal('mean returns', mu=0, sd=.01, testval=data.mean())
    sigma = pm.HalfCauchy('volatility', beta=1, testval=data.std())
    df = pm.Uniform('df', 0., 10.)

    returns = pm.StudentT('returns', nu=df, mu=mu, sd=sigma,
                       observed=data)
    
    returns_sim = pm.StudentT('returns_sim', nu=df, mu=mu, sd=sigma, shape = 504)
        
    pm.Deterministic('annual volatility',
                     returns.distribution.variance**.5 * np.sqrt(252))

    pm.Deterministic('sharpe', returns.distribution.mean /
                     returns.distribution.variance**.5 *
                     np.sqrt(252))
 
    step = pm.NUTS()
    trace = pm.sample(2000, step)

The intuition is to generate 2000 samples of 504 observation to draw the probability distribution of my VaR :

traceplot.png857×856 143 KB

As I try to estimate a 95% VaR :

percentiles = np.percentile(trace['returns_sim'], 0.05, axis = 1)

sns.distplot(percentiles)

I uploaded the full notebook here if you are interested.

Do you agree with this approach ?
It is the good way for estimating the distribution of the percentile of a parent distribution ? Perhaps PyMC3 allows a more simple way through pm.Deterministic ?

The distribution has the shape I expected and illustrates our level of uncertainty (if we had stochastic volatility I think the distribution could even be wider).

Perhaps you know some resources on this topic ?
Thanks a lot for your ideas and comments :smiley: !

Camile

2

Hi Camile,

I built the original pyfolio model and also initially had the VaR with an uncertainty estimate like you have here, but it was confusing to people so I changed it. In any case, I think your approach makes sense.

It seems like your nu parameter is bumping against the upper limit. @aseyboldt had a nice trick to model nu: BoundNormal = pm.Bound(pm.Normal.dist, lower=5); nu = BoundNormal('nu', mu=7, sd=2). That way nu is never below 5 and centered (roughly) around 7 and not constrained above.

Best,
Thomas

3

Hi Thomas,

Thanks a lot for your comment and your tip about the nu parameter.

Soon, I will try to add stochastic volatility via a Gaussian Random Walk as you suggest in one of your blog posts.

Then to go from single security to a complete portfolio I will try to add correlations and stochastic correlations (since they are not fixed either). It could be a very good way to explain to managers why standard risk measures tend to underestimate risks !

Anyway it is interesting and it is a good way to start with PyMC3 !
Thank you for your fascinating work :smile: !

Best,

Camille

4

Hi @twiecki, how would you set a shape in a bounded variable like BoundNormal?
Thank you!

5

You can set the shape with the same shape **args:

BoundNormal = pm.Bound(pm.Normal, lower=0.)
with pm.Model():
    bn = BoundNormal('bn', mu=1., sd=1., shape=10)
6

Is it possible in the case the mu and sd are two multivariate? I’m receiving:
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

7

Not yet… the fix is underway https://github.com/pymc-devs/pymc3/pull/2277

1 Like