Creating hierarchical models using 3 dimensional xarray data

Questions
1

Hi all,

I’ve been trying to create a hierarchical model using 3 dimensional data from an xarray.
I’m having trouble connected the final level to the likelihood.

In normal cases I would just have done
mu = exercise_intercept[exercise_idx] + exercise_slope[exercise_idx]*velocity.

This is however giving me an error message and I’m lost on how to solve it:
Input dimension mis-match. (input[0].shape[2] = 5, input[1].shape[2] = 15).

The code for generating the test data and model is as follows:

import pymc3 as pm
import numpy as np
import xarray as xr
import pandas as pd

# Generate test data
n_exercises = 5
n_dates = 10
n_observations = 15

exercises = [f'Exercise {i + 1}' for i in np.arange(5)]
dates = pd.date_range(start = '2020-01-01', periods = n_dates)
observations = np.arange(n_observations)

velocity_test_data = np.arange(0.15 + 0.05*n_observations, 0.15, -0.05)
velocities = np.tile(velocity_test_data, n_exercises*n_dates)
loads = list(map(lambda x: 100 + -50*x + np.random.rand()*10, velocities))

matrix_shape = (n_exercises, n_dates, n_observations)

velocity_matrix = np.reshape(velocities, matrix_shape)
load_matrix = np.reshape(loads, matrix_shape)

# Create xarray
dims = ['exercise', 'date', 'observation']

coords = {'exercise': exercises,
          'date': dates,
          'observation': observations}

dataset = xr.Dataset({'velocity': (dims, velocity_matrix),
                      'load': (dims, load_matrix)},
                     coords = coords)


# Create PyMC model
with pm.Model(coords = coords) as model:
    # Inputs
    exercise_idx = pm.Data('exercise_idx', np.arange(n_exercises), dims = 'exercise')
    date_idx = pm.Data('date_idx', np.arange(n_dates), dims = 'date')
    obs_idx = pm.Data('obs_idx', np.arange(n_observations), dims = 'observation')

    velocity = pm.Data('velocity', dataset['velocity'], dims = dims)
    load = pm.Data('load', dataset['load'], dims = dims)

    # Global parameters
    global_intercept = pm.Normal('global_intercept', mu = 100, sigma = 10)
    global_intercept_sd = pm.Exponential('global_intercept_sd', lam = 1)

    global_slope = pm.Normal('global_slope', mu = -50, sigma = 10)
    global_slope_sd = pm.Exponential('global_slope_sd', lam = 1)

    # Exercise parameters
    exercise_intercept = pm.Normal('exercise_intercept', mu = global_intercept, sigma = global_intercept_sd, dims = 'exercise')
    exercise_slope = pm.Normal('exercise_slope', mu = global_slope, sigma = global_slope_sd, dims = 'exercise')

    # Model error
    sigma = pm.Exponential('sigma', lam = 1)

    # Expected value
    mu = exercise_intercept[exercise_idx] + exercise_slope[exercise_idx]*velocity

    # Likelihood of observed values
    likelihood = pm.Normal('likelihood',
                           mu = mu,
                           sigma = sigma,
                           observed = load,
                           dims = dims)

image
image1502×438 31 KB

@OriolAbril perhaps you know how to do it? ::slight_smile:

1 Like
2

Looks like we are trying to figure out similar things:)

I’m sure I’m missing something but the problem the error message you are getting is because the shape of the exercise parameters do not have the same dimension as velocity. This could be fixed with this:

    # Exercise parameters
exercise_intercept = pm.Normal('exercise_intercept', mu = global_intercept, sigma = global_intercept_sd, dims = ('exercise','date','observation'))
exercise_slope = pm.Normal('exercise_slope', mu = global_slope, sigma = global_slope_sd, dims = ('exercise', 'date', 'observation'))

# Model error
sigma = pm.Exponential('sigma', lam = 1)

# Expected value
mu = exercise_intercept[exercise_idx] + exercise_slope[exercise_idx]*velocity[exercise_idx]
2 Likes
3

Btw what is the purpose of the date_idx and obs_idx?

My problem is still trying to figure out how I can create the xarray with dimensions from a table of data.
I have a table like this:
| region | division | team | player | x | y |

where the first four columns are categories that I would like to create a deep hierarichal model on.

2 Likes
4

They are remnants from my 1D version. In my 1D version I actually had date as a third level. You can ignore them here, they aren’t used :slight_smile:

If you have your data as a pandas data frame, you can try this:
df.set_index(['region', 'division', 'team', 'player']).to_xarray()

However, when I tried that with my real data (not the test data above) I discovered that the indexes wasn’t unique enough in my data.So instead I did the equivalent of df.groupby(['region', 'division', 'team', 'player']).max().to_xarray()

1 Like
5

Right my problem is that the players have multiple x and y values (which right now is just another row in the pandas dataframe) which seems to create difficulties since I would like to keep all x and y measurements bu there are not the same amount of data for each player.

1 Like
6

Thanks, I discovered the same after a while :slight_smile:

Updated code:

# Create PyMC model
exercise_idx = np.arange(n_exercises)

velocity = dataset['velocity']
velocity = (velocity - np.mean(velocity)) / np.std(velocity)

load = dataset['load']
load = (load - np.mean(load)) / np.std(load)

with pm.Model(coords = coords) as model:
    # Inputs
    exercise_idx = pm.Data('exercise_idx', exercise_idx, dims = 'exercise')

    velocity = pm.Data('velocity', velocity, dims = dims)
    load = pm.Data('load', load, dims = dims)

    # Global parameters
    global_intercept = pm.Normal('global_intercept', mu = 100, sigma = 1)
    global_intercept_sd = pm.Exponential('global_intercept_sd', lam = 1)

    global_slope = pm.Normal('global_slope', mu = -50, sigma = 1)
    global_slope_sd = pm.Exponential('global_slope_sd', lam = 1)

    # Exercise parameters
    exercise_intercept = pm.Normal('exercise_intercept', mu = global_intercept, sigma = global_intercept_sd, dims = dims)
    exercise_slope = pm.Normal('exercise_slope', mu = global_slope, sigma = global_slope_sd, dims = dims)

    # Model error
    sigma = pm.Exponential('sigma', lam = 1)

    # Expected value
    mu = exercise_intercept[exercise_idx] + exercise_slope[exercise_idx]*velocity[exercise_idx]

    # Likelihood of observed values
    likelihood = pm.Normal('likelihood',
                           mu = mu,
                           sigma = sigma,
                           observed = load,
                           dims = dims)
    
pm.model_to_graphviz(model)

image
image959×576 60.2 KB

Adding a level

# Create PyMC model
exercise_idx = np.arange(n_exercises)
date_exercise_idx = [exercise_idx]*n_dates

velocity = dataset['velocity']
load = dataset['load']

with pm.Model(coords = coords) as model:
    # Inputs
    date_exercise_idx = pm.Data('date_exercise_idx', date_exercise_idx, dims = ['date', 'exercise'])

    velocity = pm.Data('velocity', velocity, dims = dims)
    load = pm.Data('load', load, dims = dims)

    # Global parameters
    global_intercept = pm.Normal('global_intercept', mu = 100, sigma = 10)
    global_intercept_sd = pm.Exponential('global_intercept_sd', lam = 1)

    global_slope = pm.Normal('global_slope', mu = -50, sigma = 10)
    global_slope_sd = pm.Exponential('global_slope_sd', lam = 1)

    # Exercise parameters
    exercise_intercept = pm.Normal('exercise_intercept', mu = global_intercept, sigma = global_intercept_sd, dims = dims)
    exercise_intercept_sd = pm.Exponential('exercise_intercept_sd', lam = 1, dims = dims)

    exercise_slope = pm.Normal('exercise_slope', mu = global_slope, sigma = global_slope_sd, dims = dims)
    exercise_slope_sd = pm.Exponential('exercise_slope_sd', lam = 1, dims = dims)

    # Date parameters
    date_intercept = pm.Normal('date_intercept', mu = exercise_intercept, sigma = exercise_intercept_sd, dims = dims)
    date_slope = pm.Normal('date_slope', mu = exercise_slope, sigma = exercise_slope_sd, dims = dims)

    # Model error
    sigma = pm.Exponential('sigma', lam = 1)

    # Expected value
    mu = date_intercept[date_exercise_idx] + date_slope[date_exercise_idx]*velocity[date_exercise_idx]

    # Likelihood of observed values
    likelihood = pm.Normal('likelihood',
                           mu = mu,
                           sigma = sigma,
                           observed = load,
                           dims = dims)
    
pm.model_to_graphviz(model)

image
image1371×723 91.4 KB

Unfortunately this results in the following error:

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-207-f38b5fc3345a> in <module>()
      1 with model:
----> 2     trace = pm.sample()
      3     prior_predictions = pm.sample_prior_predictive()
      4     posterior_predictions = pm.fast_sample_posterior_predictive(trace)
      5     model_idata = az.from_pymc3(trace = trace,

8 frames
/usr/local/lib/python3.6/dist-packages/pymc3/step_methods/hmc/quadpotential.py in raise_ok(self, vmap)
    261                 errmsg.append('The derivative of RV `{}`.ravel()[{}]'
    262                               ' is zero.'.format(*name_slc[ii]))
--> 263             raise ValueError('\n'.join(errmsg))
    264 
    265         if np.any(~np.isfinite(self._stds)):

ValueError: Mass matrix contains zeros on the diagonal. 
The derivative of RV `date_slope`.ravel()[0] is zero.
...
1 Like
7

That sounds exactly like my case :slight_smile:
I would add a column using rank.
df['observation'] = df.groupby(['region', 'division', 'team', 'player']).rank(method = 'first')

Edit:
When pulling data from the xarray to the model do it via masked array xr['x'].to_masked_array() to handle NaNs

1 Like
8

Actually it looks like it didn’t work.
When looking at the inference data from the trace, I can see that the exercise parameters are actually grouped on the lowest level:

print(model_idata.posterior[['exercise_intercept', 'exercise_slope']])

<xarray.Dataset>
Dimensions:             (chain: 2, date: 7, draw: 1000, exercise: 3, observation: 6)
Coordinates:
  * chain               (chain) int64 0 1
  * exercise            (exercise) <U14 'Squat' 'Overhead Press' 'Deadlift'
  * observation         (observation) int64 1 2 3 4 5 6
  * draw                (draw) int64 0 1 2 3 4 5 6 ... 994 995 996 997 998 999
  * date                (date) <U10 '2020-02-24' '2020-02-26' ... '2020-08-10'
Data variables:
    exercise_intercept  (chain, draw, exercise, date, observation) float64 13...
    exercise_slope      (chain, draw, exercise, date, observation) float64 -8...
Attributes:
    created_at:                 2020-10-05T13:21:04.074479
    arviz_version:              0.9.0
    inference_library:          pymc3
    inference_library_version:  3.7
    sampling_time:              23.959852933883667
    tuning_steps:               1000

I expect the exercise intercept & slope to be exercise_intercept (chain, draw, exercise)
and not exercise_intercept (chain, draw, exercise, date, observation)

1 Like
10

That just seems to rearrange x,y by value and keeps the same dimension. So the connection between the coordinates (region, division, team, player) are lost.

11

Solution for 1(2?) hierarchical levels

Replaced the data with the samples from the real world:

import xarray as xr
import arviz as az
import pymc3 as pm
import numpy as np

# Create xarray with test data
coords = {'exercise': ['Squat', 'Overhead Press', 'Deadlift'],
          'date': ['2020-02-24', '2020-02-26', '2020-03-21', '2020-03-25', '2020-04-06', '2020-07-25', '2020-08-10'],
          'observation': [1, 2, 3, 4, 5, 6]}

dims = coords.keys()

velocities = [[[1.198, 1.042, 0.875, 0.735, 0.574, 0.552],
               [1.261, 0.993, 0.857, 0.828, 0.624, 0.599],
               [1.224, 1.028, 0.990, 0.742, 0.595, 0.427],
               [1.112, 0.999, 0.865, 0.751, 0.607, 0.404],
               [1.157, 1.010, 0.849, 0.716, 0.593, 0.536],
               [1.179, 1.060, 0.898, 0.783, 0.615, 0.501],
               [1.209, 1.192, 0.979, 1.025, 0.875, 0.887]],
              
              [[0.911, 0.933, 0.779, 0.629, 0.528, 0.409],
               [1.004, 0.863, 0.770, 0.611, 0.511, 0.376],
               [0.980, 0.828, 0.766, 0.611, 0.529, 0.349],
               [1.024, 0.933, 0.841, 0.734, 0.551, 0.287],
               [0.985, 0.852, 0.599, 0.522, 0.313, 0.234],
               [0.996, 0.763, 0.758, 0.542, 0.463, 0.378],
               [1.066, 0.915, 0.786, 0.686, 0.565, 0.429]],
              
              [[0.654, 1.004, 0.727, 0.483, 0.344, 0.317],
               [0.885, 0.738, 0.577, 0.495, 0.335, 0.291],
               [0.749, 0.695, 0.539, 0.461, 0.395, 0.279],
               [0.801, 0.548, 0.404, 0.424, 0.337, 0.338],
               [0.770, 0.642, 0.602, 0.493, 0.394, 0.290],
               [0.766, 0.545, 0.426, 0.431, 0.349, 0.329],
               [0.787, 0.640, 0.480, 0.401, 0.395, 0.304]]]

loads = [[[20.0,  40.0,  60.0,  80.0, 100.0, 110.0],
          [20.0,  40.0,  60.0,  80.0, 100.0, 110.0],
          [20.0,  40.0,  60.0,  80.0, 100.0, 117.5],
          [20.0,  40.0,  60.0,  80.0, 100.0, 115.0],
          [20.0,  40.0,  60.0,  80.0, 100.0, 110.0],
          [20.0,  40.0,  60.0,  80.0, 100.0, 110.0],
          [20.0,  30.0,  40.0,  50.0,  60.0,  70.0]],
         
         [[20.0,  25.0,  30.0,  35.0,  40.0,  45.0],
          [20.0,  25.0,  30.0,  35.0,  40.0,  45.0],
          [20.0,  25.0,  30.0,  35.0,  40.0,  45.0],
          [20.0,  25.0,  30.0,  35.0,  40.0,  45.0],
          [20.0,  30.0,  40.0,  45.0,  50.0,  52.5],
          [20.0,  30.0,  35.0,  40.0,  42.5,  45.0],
          [20.0,  25.0,  30.0,  35.0,  40.0,  45.0]],
         
         [[60.0,  80.0, 100.0, 120.0, 140.0, 145.0],
          [60.0,  80.0, 100.0, 120.0, 140.0, 145.0],
          [60.0,  80.0, 100.0, 120.0, 127.5, 140.0],
          [60.0, 100.0, 120.0, 125.0, 140.0, 145.0],
          [60.0,  80.0, 100.0, 120.0, 130.0, 140.0],
          [60.0, 100.0, 120.0, 125.0, 130.0, 132.5],
          [70.0,  90.0, 120.0, 135.0, 140.0, 150.0]]]

dataset = xr.Dataset({'velocity': (dims, velocities),
                      'load': (dims, loads)},
                     coords = coords)

dataset['velocity_std'] = (dataset['velocity'] - dataset['velocity'].mean())/dataset['velocity'].std()
dataset['load_std'] = (dataset['load'] - dataset['load'].mean())/dataset['load'].std()

dataset

New model:

# Create PyMC
n_exercises = dataset.dims['exercise']
n_dates = dataset.dims['date']
n_observations = dataset.dims['observation']

exercise_idx = [[[i]*n_observations for j in np.arange(n_dates)] for i in np.arange(n_exercises)]

velocity = dataset['velocity_std']
load = dataset['load_std']

with pm.Model(coords = coords) as model:
    # Inputs
    exercise_idx_shared = pm.Data('exercise_idx', exercise_idx, dims = dims)

    velocity_shared = pm.Data('velocity', velocity, dims = dims)
    load_shared = pm.Data('load', load, dims = dims)

    # Global parameters
    global_intercept = pm.Normal('global_intercept', mu = 0, sigma = 1)
    global_intercept_sd = pm.Exponential('global_intercept_sd', lam = 1)

    global_slope = pm.Normal('global_slope', mu = 0, sigma = 1)
    global_slope_sd = pm.Exponential('global_slope_sd', lam = 1)

    # Exercise parameters
    exercise_intercept = pm.Normal('exercise_intercept', mu = global_intercept, sigma = global_intercept_sd, dims = 'exercise')
    exercise_slope = pm.Normal('exercise_slope', mu = global_slope, sigma = global_slope_sd, dims = 'exercise')

    # Model error
    sigma = pm.Exponential('sigma', lam = 1)

    # Expected value
    mu = exercise_intercept[exercise_idx_shared] + exercise_slope[exercise_idx_shared]*velocity_shared

    # Likelihood of observed values
    likelihood = pm.Normal('likelihood',
                           mu = mu,
                           sigma = sigma,
                           observed = load_shared,
                           dims = dims)

image
image1140×580 62.4 KB

As I understand, the trick was to get the exercise_idx down to the lowest level in the matrix:

exercise_idx = [[[i]*n_observations for j in np.arange(n_dates)] for i in np.arange(n_exercises)]

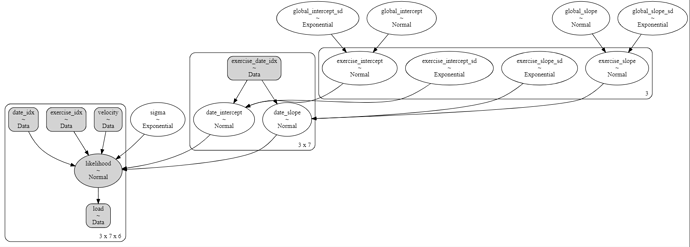
Solution for 2(3?) level hierarchy
The key was once again the indexing. In addition to exercise_idx, the equivivalent for date_idx was needed, and the intermediate indexing exercise_date_idx. The first ones are the full array with the values replaced by the index number of the corresponding coord. The intermediate index list brings the index from the upper (exercise) coord down to the current (date) coord.

# Create PyMC
n_exercises = dataset.dims['exercise']
n_dates = dataset.dims['date']
n_observations = dataset.dims['observation']

exercise_date_idx = [[i]*n_dates for i in np.arange(n_exercises)]
exercise_idx = [[[i]*n_observations for j in np.arange(n_dates)] for i in np.arange(n_exercises)]
date_idx = [[[j]*n_observations for j in np.arange(n_dates)] for i in np.arange(n_exercises)]

velocity = dataset['velocity_std']
load = dataset['load_std']

with pm.Model(coords = coords) as model:
    # Inputs
    exercise_date_idx_shared = pm.Data('exercise_date_idx', exercise_date_idx, dims = ['exercise', 'date'])
    exercise_idx_shared = pm.Data('exercise_idx', exercise_idx, dims = dims)
    date_idx_shared = pm.Data('date_idx', date_idx, dims = dims)

    velocity_shared = pm.Data('velocity', velocity, dims = dims)
    load_shared = pm.Data('load', load, dims = dims)

    # Global parameters
    global_intercept = pm.Normal('global_intercept', mu = 0, sigma = 1)
    global_intercept_sd = pm.Exponential('global_intercept_sd', lam = 1)

    global_slope = pm.Normal('global_slope', mu = 0, sigma = 1)
    global_slope_sd = pm.Exponential('global_slope_sd', lam = 1)

    # Exercise parameters
    exercise_intercept = pm.Normal('exercise_intercept', mu = global_intercept, sigma = global_intercept_sd, dims = 'exercise')
    exercise_intercept_sd = pm.Exponential('exercise_intercept_sd', lam = 1, dims = 'exercise')

    exercise_slope = pm.Normal('exercise_slope', mu = global_slope, sigma = global_slope_sd, dims = 'exercise')
    exercise_slope_sd = pm.Exponential('exercise_slope_sd', lam = 1, dims = 'exercise')
    
    # Date parameters
    date_intercept = pm.Normal('date_intercept', mu = exercise_intercept[exercise_date_idx_shared], sigma = exercise_intercept_sd[exercise_date_idx_shared], dims = ['exercise', 'date'])
    date_slope = pm.Normal('date_slope', mu = exercise_slope[exercise_date_idx_shared], sigma = exercise_slope_sd[exercise_date_idx_shared], dims = ['exercise', 'date'])

    # Model error
    sigma = pm.Exponential('sigma', lam = 1)

    # Expected value
    mu = date_intercept[exercise_idx_shared, date_idx_shared] + date_slope[exercise_idx_shared, date_idx_shared]*velocity_shared

    # Likelihood of observed values
    likelihood = pm.Normal('likelihood',
                           mu = mu,
                           sigma = sigma,
                           observed = load_shared,
                           dims = dims)

image
image1633×585 38.2 KB

8 Likes
12

Thank you so much for sharing this!

2 Likes
13

You mentioned using to_masked_array in the other post, could you give an example to when that is useful?

I tried this approach for my data but I don’t think this will work for me, I have really no way of knowing the length of my observations for the last level so the only way around this using xarray I think, would be to create another coordinate for all observations, that looks good but I run out of memory since the arrays become extremely sparse. There does not seem to be much information regarding sparse matrices with either pymc3 or xarray.

Another thing I am wondering about the index loops have you made sure your data is sorted in a certain order or does xarray take care of that?

1 Like
14

So this only works if there are no nan values right?

If I randomly replace some of the observed values with nans, the likelihood is equal to nan in the prior checks.

15

I’ll give you a detailed answer in a few hours, when I have more time.

But in short, to_masked_array() is to hide the NaN values from PyMC. However, I’ve found that it’s not working, so use np.ma.masked_equal(xr['field'].fillna(-999), -999) for the intended result. Just make sure -999 isn’t a value that you will have in your data :slight_smile:

1 Like
16

Thanks, I think I’ll need more details :sweat_smile:

Edit: Seems to be working although the sampling is very slow.

17

I noticed the same, it went from 5min to 6(!)h…
and when looking closer, it doesn’t seem like it is masking anything, I think PyMC just sees -999 as the value. Take a look at the likelihood below.

Using -1 as filler:

global_intercept                -0.92
global_intercept_sd_log__       -1.06
global_slope                    -0.92
global_slope_sd_log__           -1.06
exercise_intercept              -1.66
exercise_intercept_sd_log__     -3.18
exercise_slope                  -1.66
exercise_slope_sd_log__         -3.18
date_intercept                 -11.60
date_slope                     -11.60
sigma_log__                     -1.06
likelihood                    -200.73
Name: Log-probability of test_point, dtype: float64

Using -999 as filler:

global_intercept                    -0.92
global_intercept_sd_log__           -1.06
global_slope                        -0.92
global_slope_sd_log__               -1.06
exercise_intercept                  -1.66
exercise_intercept_sd_log__         -3.18
exercise_slope                      -1.66
exercise_slope_sd_log__             -3.18
date_intercept                     -11.60
date_slope                         -11.60
sigma_log__                         -1.06
likelihood                    -6231819.43
Name: Log-probability of test_point, dtype: float64

The radically different number for the likelihood is what makes me suspect that no masking is taking place. This also explains why the likelihood remains as NaN when using either to_masked_array() or np.ma.masked_invalid().

18

Good point, I assumed that dataset['coord'].values are returned in the same order as in the matrix for dataset['velocity']

A nicer way to generate the indexes might be this:

shape = dataset['velocity'].shape
level_0_idx_by_level_1 = [[i]*np.prod(shape[1]) for i in np.arange(shape[0])]
level_0_idx_by_lowest_level = np.reshape([[i]*np.prod(shape[1:]) for i in np.arange(shape[0])], shape)
level_1_idx_by_lowest_level = np.reshape([[i]*np.prod(shape[2:]) for i in np.arange(shape[1])]*shape[0], shape)

It still assumes the ordering though.

19

Did you follow this up further?

20

Sorry, no, I’ve been tied up in work, so I haven’t had time.

21

Sorry to bump this once more, but did you get this to work?