Errors-in-variables model in PyMC3

[MoUG]

I’m currently trying to implement an errors-in-variables model (a regression model that accounts for errors in the independent variables) in PyMC3.
In a recently published paper (https://arxiv.org/pdf/1906.03989.pdf) I’ve read that

"Except for the simplest case of linear regression [29], EIV modeling almost always
requires auxiliary information or data to correct the mismeasurement bias in estimation.
[…] However, without additional data, Bayesian EIV
modeling is currently the most powerful and flexible approach, as it allows incorporating
additional information in the form of distributional assumptions [15].

So let’s say we have a simple linear errors-in-variables model:

where α and β are the parameters of interest, ε_t and η_t are the errors and x_t^* denotes the true but unobserved regressor.

First I create some dummy data and add some error:

import numpy as np
intercept = 0 
gradient = 2.5
size = 10000

x_true = np.array(np.linspace(0,1,size))
y_true = intercept + gradient * x_true

# adding noise to data
x = x_true + np.random.normal(loc=0, scale=0.5, size=size)
y = y_true + np.random.normal(loc=0, scale=0.5, size=size)

And then I created my model (reproduced it from Using random variables as `observed` · Issue #2226 · pymc-devs/pymc · GitHub and made some adjustments), where I used high sd’s to get noninformative priors and modeled the “true” regressor x^* as a random variable, independend from the measurement error:

import pymc3 as pm

    with pm.Model() as eiv_model:
    # Define priors
    intercept = pm.Normal('intercept', mu=0, sd=20)
    gradient = pm.Normal('gradient', mu=0, sd=20)
    
    sigma_x = pm.HalfNormal('sigma_x', sd=20)
    sigma_y = pm.HalfNormal('sigma_y', sd=20)

    true_x = pm.Normal('true_x', mu=0, sd=10)
    likelihood_x = pm.Normal('x', mu=true_x, sd=sigma_x, observed=x)
    true_y = pm.Deterministic('true_y', intercept + gradient * true_x)
    likelihood_y = pm.Normal('y', mu=true_y, sd=sigma_y, observed=y)

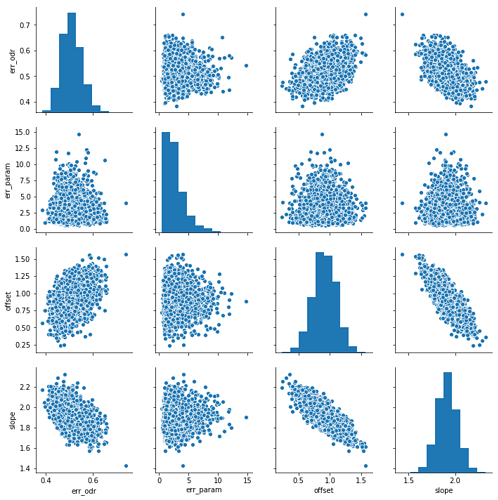
As a result I get:

And now I have some questions:

1. Is this model a representative Bayesian errors-in-variables model or is there some bias I’m just not seeing?
2. The inferences of the errors, true_x and true_y seems reasonable, but the uncertainty of the intercept and gradient is quite big. Is there a valid way to reduce that uncertainty if all that’s given are the noisy measurements of x and y?
3. In the model from Using random variables as `observed` · Issue #2226 · pymc-devs/pymc · GitHub, the shape paramter is used for modelling the true regressor x, but this is only necessary for multivariate models, right?
4. Is it possible to modify the model so, that the result corresponds to an orthogonal distance regression model? How would the priors be formulated then?

I’m thankful for any advice, since I’m new to Bayesian inference and probabilistic programming.

[chartl]

I think its easiest to think of errors-in-variables as a repeated-measures model, and then take the number of replicates to be 1 so that:

x_{t,i} \sim N(x_t, \sigma^2_x)
y_{t,i} \sim N(\alpha + \beta x_t, \sigma^2_y)

Then x_t should be a vector and not, as in your case, a scalar, so add shape=x.shape[0] to true_x.

This explains why the intercept and gradient do not differ much from their prior. As true_x was a scalar, it basically estimates the mean and standard deviation of your data (x), so the effective number of samples you’re using is 1 instead of 10000.

With multiple replicates, you have a good amount of information to constrain the variance \sigma_x^2. When you take the number of replicates to 1, you lose the ability to decompose the residual variance into \sigma_x^2 and \sigma_y^2. This is a consequence of the fact that the model is underdetermined; so with this parametrization you should expect divergences to occur as a matter of course.

ODR is a re-parameterization under an assumed variance ratio (\sigma_y^2 = c \cdot \sigma_x^2; c=1 corresponds to ODR, c \neq 1 to weighted ODR). Thus, for classical ODR, the only change is to replace sigma_x and sigma_y with a single sigma_odr.

One final note: Because the variance of your x data is large compared to the range, there is a lot of wiggle room between the slope and the intercept, so even though the true value of the intercept is 0, the marginal mean winds up being close to 1.

Increasing the range of x to np.linspace(0, 10, size) results in a better ability to partition between the slope and intercept terms.

with pm.Model() as model:
    err_odr = pm.HalfNormal('err_odr', 5.)
    err_param = pm.HalfNormal('err_param', 5.)
    x_lat = pm.Normal('x_mu', 0, 5., shape=x.shape[0])
    x_obs = pm.Normal('x_obs', mu=x_lat, sd=err_odr, observed=x, shape=x.shape[0])
    offset = pm.Normal('offset', 0, err_param)
    slope = pm.Normal('slope', 0, err_param)
    y_pred = pm.Deterministic('y_pred', offset + slope * x_lat)
    y_obs = pm.Normal('y', mu=y_pred, sd=err_odr, observed=y)
    
    trace = pm.sample(800, tune=1500, chains=4, cores=3, init='jitter+adapt_diag')

[MoUG]

Thank you for this detailed answer, I think that cleared my misunderstandings!

[thiberio]

Hi,

if I have unequal errors among my observations can I add “shape=x.shape[0]” to the err_odr definition to assign a distinct error measure for each point?
err_odr = pm.HalfNormal('err_odr', 5., shape=x.shape[0])