Estimating Two survivals curves at the same time with a cure fraction

1

I am trying to estimate a survival curve with cure fraction.

I would like to use the censor distribution function. However, I don’t know how to work the cure fraction into the analysis.

S = p + (1-p) * Su (where p is the percent who are cured).

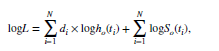
image

image

image

I did an example where I entered the mathematical equations for an exponential distributions. However, I would rather use the censored distributions. I don’t see how you get a statistical function like for instance in excel where you enter the parameters, the x value, and it returns a value either from the pdf or cdf. I’m having trouble figuring how to do this in PyMC.

Below is working code for a model with RFS and PFS for two arms and two treatments.


# Helper functions

def Su(lambda_,t):
    return pm.math.exp(-lambda_ * t)

def So(lambda_,t,p):
    return p + (1-p)*Su(lambda_,t)

def fu (lambda_,t):    
    return lambda_*pm.math.exp(-lambda_ * t)

def ho (lambda_,t,p):    
    return (1-p)*fu(lambda_,t) / (p + (1-p)*Su(lambda_,t))


# Data 
dataSOC=osrfs.query('treatment=="SOC"')

T_OS_SOC=dataSOC["os"].to_numpy()
E_OS_SOC=dataSOC["os_event"].to_numpy()

T_RFS_SOC=dataSOC["rfs"].to_numpy()
E_RFS_SOC=dataSOC["rfs_event"].to_numpy()

dataFLIN=osrfs.query('treatment=="SOC FLIN"')

T_OS_FLIN=dataFLIN["os"].to_numpy()
E_OS_FLIN=dataFLIN["os_event"].to_numpy()

T_RFS_FLIN=dataFLIN["rfs"].to_numpy()
E_RFS_FLIN=dataFLIN["rfs_event"].to_numpy()

K=2
J=2

coords={'endpoints': ['OS','RFS'], 'treatments': ['SOC', 'SOC FLIN']}

# Model

from pymc.math import exp, log
with pm.Model() as model_2:
    
    # p global 
    p_global=pm.Beta("p_global",alpha=1,beta=1)
    beta_global=pm.Deterministic("beta_global",pm.math.logit(p_global))
    
    # Priors by treatment
    vk=pm.Normal("vk",mu=beta_global, sigma=0.2,shape=(K,1))  
    sk=pm.HalfNormal("sk",2.5,shape=(K,1))

    lind_SOC=pm.Normal("lind_SOC",-1.0,sigma=5);
    lind_FLIN=pm.Normal("lind_FLIN",-1.0,sigma=5);

    d_SOC=pm.Deterministic("d_SOC",pm.math.invlogit(lind_SOC))
    d_FLIN=pm.Deterministic("d_FLIN",pm.math.invlogit(lind_FLIN))
    
    linp_SOC=pm.Normal("linp_SOC",vk[0],sk[0])
    p_SOC=pm.Deterministic("p_SOC",pm.math.invlogit(linp_SOC))

    linp_FLIN=pm.Normal("linp_FLIN",vk[1],sk[1])
    p_FLIN=pm.Deterministic("p_FLIN",pm.math.invlogit(linp_FLIN))

    beta0_OS_SOC=pm.Normal("beta0_OS_SOC",mu=0,sigma=100)
    lambda_OS_SOC=pm.math.exp(-(beta0_OS_SOC))
    OS_SOC = pm.Potential("OS_SOC",E_OS_SOC*log(ho(lambda_OS_SOC,T_OS_SOC,(p_SOC+d_SOC)))+log(So(lambda_OS_SOC,T_OS_SOC,(p_SOC+d_SOC))))

    beta0_OS_FLIN=pm.Normal("beta0_OS_FLIN",mu=0,sigma=100)
    lambda_OS_FLIN=pm.math.exp(-(beta0_OS_FLIN))
    OS_FLIN = pm.Potential("OS_FLIN",E_OS_FLIN*log(ho(lambda_OS_FLIN,T_OS_FLIN,(p_FLIN+d_FLIN)))+log(So(lambda_OS_FLIN,T_OS_FLIN,(p_FLIN+d_FLIN))))

    beta0_RFS_SOC=pm.Normal("beta0_RFS_SOC",mu=0,sigma=100)
    lambda_RFS_SOC=pm.math.exp(-(beta0_RFS_SOC))
    RFS_SOC = pm.Potential("RFS_SOC",E_RFS_SOC*log(ho(lambda_RFS_SOC,T_RFS_SOC,p_SOC))+log(So(lambda_RFS_SOC,T_RFS_SOC,p_SOC)))

    beta0_RFS_FLIN=pm.Normal("beta0_RFS_FLIN",mu=0,sigma=100)
    lambda_RFS_FLIN=pm.math.exp(-(beta0_RFS_FLIN))
    RFS_FLIN = pm.Potential("RFS_FLIN",E_RFS_FLIN*log(ho(lambda_RFS_FLIN,T_RFS_FLIN,p_FLIN))+log(So(lambda_RFS_FLIN,T_RFS_FLIN,p_FLIN))) 
    
    data = pm.sample(draws=10000,tune=5000,nuts_sampler="nutpie",cores=20,target_accept=0.99)