Richard McElreath in his book Statistical Rethinking Chapter 13 models varying intercepts where categories covary not in a discrete way but based on a continuous variable. In his example he uses euclidean distance as the metric of similarity between data generating points. He then uses this kernel to model the covaration in a MvN distribution between data generating points.
Here is the code in pymc3 for his model:
with pm.Model() as m_13_7_:
# kernel hyperparameters
etasq = pm.HalfCauchy(‘etasq’, 1)
rhosq = pm.HalfCauchy(‘rhosq’, 1)
# kernel function
Kij = etasq * (tt.exp(-rhosq * Dmatsq) + np.diag([.01] * Nsociety))
g = pm.MvNormal('g', mu=np.zeros(Nsociety), cov=Kij, shape=Nsociety)
# priors on intercept / slopes
a = pm.Normal('a', 0, 10)
bp = pm.Normal('bp', 0, 1)
# linear model
lam = pm.math.exp(a + g[dk.society.values] + bp * dk.logpop)
# likelihood
obs = pm.Poisson(‘total_tools’, lam, observed=dk.total_tools)
trace_13_7_ = pm.sample(1000, tune=1000)
I am using a similar style of model and am hoping for speed ups using the marginalsparse method.
How would one reparameterize this inside of the pm.gp class? Or would it be better/easier to get pymc3 to recognize a sparse covariance matrix?
Thanks.
I realize you’d want to put the covariance function inside the model by using pm.gp.cov. But when you also include the marginal_likelihood method it wants you to give it both x and y values, but my y values haven’t been calculated yet. Here is an example of my failed reparameterizing:
with pm.Model() as m_13_7_reparam:
etasq = pm.HalfCauchy(‘etasq’, 1)
rhosq = pm.HalfCauchy(‘rhosq’, 1)
Kij = etasq * pm.gp.cov.ExpQuad(2,ls=rhosq) # two dimensions
g = pm.gp.MarginalSparse('g',cov_func=Kij)
# priors
a = pm.Normal('a', 0, 10)
bp = pm.Normal('bp', 0, 1)
# linear model
lam = pm.math.exp(a + g[dk.society.values] + bp * dk.logpop)
# likelihood
obs = pm.Poisson('total_tools', lam, observed=dk.total_tools)
# marginal likelihood
g = gp.marginal_likelihood('g', X=Dmat_, y=dk.total_tools ,noise=.5)
# inference
trace_13_7_reparam = pm.sample(1000, tune=1000)
To be clear I want to model some output function say f* not only in terms of the metric of similarity x that goes into the kernel function k(x,x) but also in terms of a linear submodel at each point x. So its like a hiearchical linear regression but with shrinkage not solely due to discrete membership to a larger group X_{[{1...i]}} but also in a continuous sense by the metric of similarity modeled by k(x,x).
I dont think this could be done easily under the current API, as ExpQuad kernel needs raw x instead of distance matrix (ie, Dmat), and the same goes for SparseApprox as it need actually location x to set up the induce point.
It would be possible if instead of having the distance matrix Dmat_, we have the raw coordinate of the islands.
First of all thanks for your time and input!
Yes. Thanks for pointing that out. I do have Lat Long coordinates for my problem. Then Ill just need to manipulate the ExPQuad kernel method to also do some trigonometry. Either way, my conceptual problem right now is how to include the linear sub-model inside of the GP. Would this be considered a mean function m(x',x') ? Somthing like GP(0,k(x,x) ) + X' \beta where \beta are parameters to be learned from the data and X' is the design matrix. Williams and Rassmussen 2006 on p.46 equation 240 talk of adding a linear model as a mean function, however, they do so in the context of modeling the residuals. Do you think there are significant time improvements by reparameterizing inside the SparseApprox method?
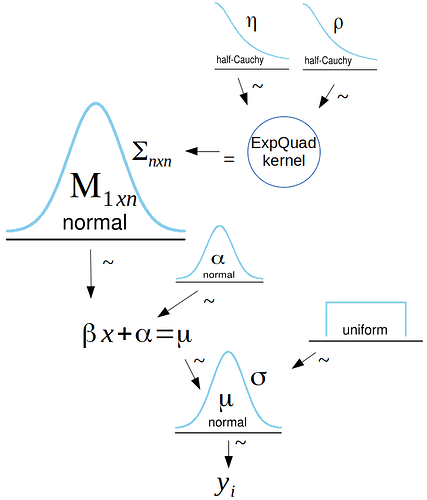
Here is a kruschke diagram of the model I am trying to reparameterize:
You can code it into the GP as a mean function, actually in gp.Latent it is default to reparameterized so it is just like GP(0, k(x, x)) + Xb (https://github.com/pymc-devs/pymc3/blob/c760a85299693ea81c39081077f982916a5055a9/pymc3/gp/gp.py#L109), but since you are going to use sparse approximation as well, it is easier probably to pop the linear prediction out and add it specifically after the GP is initialized.
@junpenglao Thanks for your help! So when I call the pm.gp.MarginalSparse().marginallikelihod method it requires parameter ‘y’ to measure the fit of the GP. However, I am currently modelling fit with the linear submodel and therefore y in my parameterization is a pymc3.model.freeRV. Can one put random variables inside the marginallikelihod method as the parameter to model fit? Edit: I think I just found it… is_observed parameter sets y as an array of data or a RV.
1 Like
So I think I have my model reparameterized in terms of the pm.gp class. Thanks for your help @junpenglao! But I am realizing now that well MarginalSparse has many features it doesn’t seem to accommodate easily a predefined metric by which to eliminate correlations between points in X. As I understand it I don’t want to use inducing points (whereby I reduce the size of the Covariance matrix), but instead use all of X, but only consider some of the correlations between elements of X e.g. Cov(xi, xj) for some i j. To be clear a covariance matrix with the original dimensions of the data n x n with a bunch of zeros in it. Is this easily accomplished in MarginalSparse?
Actually, in his book, Osvaldo Martin ported McElreath’s islands example to PyMC3 using the pm.gp class. I don’t know if it answers your questions, but it might give you some pointers.
1 Like
Awesome! Thanks @AlexAndorra!
1 Like
Hey @AlexAndorra . This doesn’t solve my particular problem as I’ve already got it coded in the pm.gp class and am now trying to do a sparse GP by not using inducing points, but by using an an nxn sparse covariance matrix. But this is likely helpful to others who find this question, so I’ll leave it as the solution. Thanks!
1 Like
The MarginalSparse class represents a GP implementation where you’re using inducing points, and you’ve integrated out the GP f (which I think you need explicitly since it is your intercepts). I think I understand that the way you have it coded originally works, but that you’re looking for speedups. How big is K? I think trying to use a sparse covariance matrix will only help you if K is very large (and has many zeros), and your slowdown is due to repeatedly inverting K. If K is too big, I suspect you’ll also run into memory issues quickly. If K is reasonably sized and sampling what is slow, it could be because NUTS is having a hard time with strong correlations in your posterior. This seems pretty common for GPs because the lengthscale has a strong interaction with other parameters. I suspect that’s the case for this model. The best way to speed sampling up is to use more informative priors on the GP hyperparameters, lengthscale and eta. Instead of HalfCauchy, you could use Gamma’s.
1 Like
Hi @bwengals . Thanks for the pointers!
K is 4000 x 4000. Which should be reasonable? It takes about 12 GB of RAM and 4 days to run on my laptop (wish I had access to something better), which is on the edge of me being able to use it for my case. It sure seems its due to repeated inversions of this matrix when sampling as I have tried stronger priors (although not strong gammas-will give that a try). I have also set either eta or lengthscale to fixed values and I get basically no speed ups unless I fix both, which leads me to believe its mostly due to the matrix inversions. But I am fairly new to mcmc so correct me if this logic doesn’t sound right.
I have used inducing points in the marginalsparse method, however they don’t really make sense for my problem as I understand it (and I take your point about integrating over f ). As I want to infer something about each x in K. I do not need all the correlations between x_i's so I could easily make K 80-90% sparse and this could actually help in the inference in my case. What are your thoughts about representing it as a sparse matrix to theano? Are there speed ups here?
Right now I am doing sensitivity analyses by fixing the kernel hyperparameters  So any speed up that would allow me to sample the posterior of them would be awesome!
So any speed up that would allow me to sample the posterior of them would be awesome! 
Thanks for taking a look at this!
Brian
 So any speed up that would allow me to sample the posterior of them would be awesome!
So any speed up that would allow me to sample the posterior of them would be awesome! 