Help with model for estimating difference in proportions

[jhrcook]

Hello, I have a problem that I think is relatively simple, but can’t seem to figure out exactly what to do.

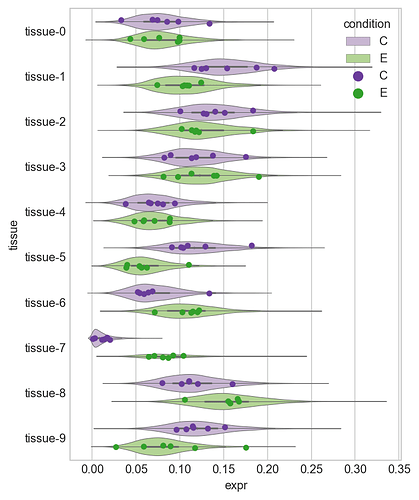
I have measured a protein’s expression in two groups, a control and experimental, across 10 tissues. I have measured the expression in 6 replicates for each condition across all 10 tissues. Therefore, I have 10 \times 6 \times 2 measurements. The values are all greater than or equal to 0 (i.e. 0 or positive) and the sum of the values for each replicate sum to 1.

I want to know if the expression of the protein is different between control and experiment in each tissue.

Because of the constraint on the values being \ge0 and summing to 1 across replicates, I think I should use a Dirichlet likelihood, but can’t put anything too useful together so far.

Here is code to generate some toy data:

N_TISSUES = 10
N_REPS = 6
CONDITIONS = ["C", "E"]

TISSUES = [f"tissue-{i}" for i in range(N_TISSUES)]
REPS = [f"{CONDITIONS[0]}-{i}" for i in range(N_REPS)]
REPS += [f"{CONDITIONS[1]}-{i}" for i in range(N_REPS)]

np.random.seed(909)
ctrl_tissue_props = np.random.uniform(0, 1, N_TISSUES)
ctrl_tissue_props = ctrl_tissue_props / np.sum(ctrl_tissue_props)
expt_tissue_props = np.random.uniform(0, 1, N_TISSUES)
expt_tissue_props = expt_tissue_props / np.sum(expt_tissue_props)

print("Real proportions for each tissue:")
print(np.vstack([ctrl_tissue_props, expt_tissue_props]).round(3))
#> Real proportions for each tissue:
#> [[0.134 0.021 0.067 0.104 0.054 0.124 0.225 0.096 0.021 0.153]
#>  [0.044 0.189 0.004 0.049 0.036 0.18  0.138 0.137 0.185 0.036]]

_ctrl_data = np.random.dirichlet(ctrl_tissue_props*100, N_REPS).T
_expt_data = np.random.dirichlet(expt_tissue_props*100, N_REPS).T

expr_data = pd.DataFrame(np.hstack([_ctrl_data, _expt_data]), columns=REPS).assign(tissue=TISSUES).set_index("tissue")
expr_data.round(3)

The sum across tissues (rows) for each replicate (columns) is equal to 1:

expr_data.values.sum(axis=0)
#> array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

My plan is to eventually add hierarchical relationships and add another dimension because I have measured the expression of more proteins, but I would greatly appreciate anyone’s help to get me started on the right path. Thank you!

[jhrcook]

I think I figured it out, but would definitely appreciate any further input. Basically, I was very close with using the Dirichlet distribution for the likelihood, just needed to get the correct link funtion for a generalized linear model. Here is the final model, using the data generated above except the Dirichlet needed the data transposed.

expr_data = expr_data.T

coords = {"tissue": TISSUES, "replicate": REPS}

intercept = np.ones_like(expr_data)
x_expt_cond = np.vstack([np.zeros((N_REPS, N_TISSUES)), np.ones((N_REPS, N_TISSUES))])

with pm.Model(coords=coords) as dirichlet_reg:
    a = pm.Normal("a", 0, 5, dims=("tissue",))
    b = pm.Normal("b", 0, 2.5, dims=("tissue",))
    eta = pm.Deterministic(
        "eta",
        a[None, :] * intercept + b[None, :] * x_expt_cond,
        dims=("replicate", "tissue"),
    )
    mu = pm.Deterministic("mu", pm.math.exp(eta), dims=("replicate", "tissue"))
    y = pm.Dirichlet("y", mu, observed=expr_data.values, dims=("replicate", "tissue"))

pm.model_to_graphviz(dirichlet_reg)

The original proportions were well estimated:

And the posterior predictive distributions were fairly accurate:

I have put the full code as a GitHub gist: Dirichlet regression in PyMC · GitHub

[ricardoV94]

Thank you so much for sharing the solution!