How to create a Vector Autoregressive AR1?

Questions
1

I was wondering how do I create a multivariate AR1. As you will see below, if I try to do an AR1 with one dimension I get normal results, but the moment I scale up to 2 dimensions my results get very wacky (even though the two dimensions are independent).

with pm.Model() as warr_model:
       warr_tau = pm.HalfNormal('warr_tau',sigma = 10)

       warr_coef = pm.Normal('warr_coef',mu = 1, sigma = 20)

       warr_ar1 = pm.AR1('warr_ar1',k = warr_coef, tau_e = warr_tau, shape = len(warr_fg3m))![21%20pm|690x266](upload://yHYqSwFRqNf4GkfNM5mIHTh3ATa.png) 

       game_sd = pm.HalfNormal("game_sd", sigma = 20)

       y = pm.Normal('y',mu = warr_ar1,sigma = game_sd, observed = warr_fg3m)

I get normal results, as seen right here

21%20pm
21%20pm1250×482 51.6 KB

If I do someething similar with New Orleans I also get normal results:

25%20pm
25%20pm1722×470 56.9 KB

However, when I try to combine these two into a multivariate AR1 I get wacky results. Note in the code below, the results of New Orleans and the Warriors is independent.

with pm.Model() as warr_nola:
# This iss a combined model where we are doing analysis on both NOLA and Warriors
        comb_tau = pm.HalfNormal('comb_tau',sigma = 10,shape =2)

       comb_coef = pm.Normal('comb_coef',mu = 1, sigma = 20, shape = 2 )

       comb_ar1 = pm.AR1('comb_ar1',k = comb_coef, tau_e = comb_tau, shape = (40,2))

       comb_sd = pm.HalfNormal("comb_sd", sigma = 20,shape = 2)

       y_comb = pm.Normal('y_comb',mu = comb_ar1,sigma = comb_sd, observed = np.stack([nola_fg3m,warr_fg3m],axis =1))

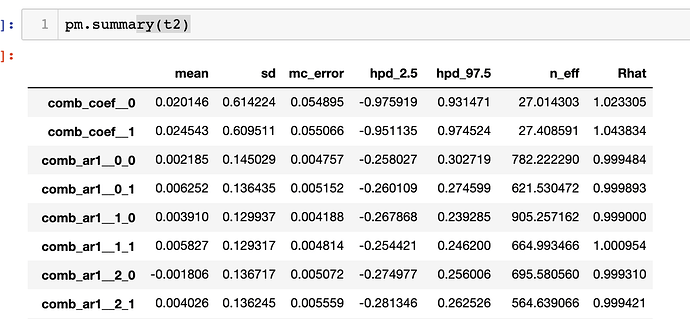
If I sample from this distribution, I get pretty wacky results that are significantly different:

51%20pm
51%20pm1296×600 73.3 KB

Can someone please explain what’s going wrong. Also the wierdness is combing from the fact that my k-coefficient goes from ~.98 to ~.02 when I change from a univariate to a multivariate case.
[/quote]

2

For anyone that might be facing a similar problem, the key is to use the AR model instead of the AR1. Just set the number of coefficients in the AR model to 1. Thus the shape of rho would be (1, n_vars).