How to do partially pooled linear regression when x[0] == 0 for all instances where x[1] == "specific-class"?

1

Consider the case where I am running a program with no logging or with one of several logging engines. If any of the logging engines are enabled, the program generates some log lines and sends them to the engine, each of which carries an associated overhead; if no logging engine is enabled, the program generates no log lines or overhead are created at all.

I am using the following model:

inherent_runtime ~ Exponential(100)

pooled_overhead_per_line_mean ~ Exponential(1e-3)
pooled_overhead_per_line_stddev ~ Exponential(1e-4)
overhead_per_line[logging_engine] ~ Normal(
    mu=pooled_overhead_per_line_mean,
    sigma=pooled_overhead_per_line_stddev)

runtime_std ~ Exponential(1/1e-2)
runtime ~ Normal(
    inherent_runtime + num_ops * overhead_per_line[logging_engine],
    runtime_std)

Observations are triples of (runtime, num_lines, logging_engine). So far, so good.

The problem is that when logging_engine == "no logging", num_log_lines will always be zero, and I believe overhead_per_line["no logging"] will be underconstrained because it does not affect any observed quantity!

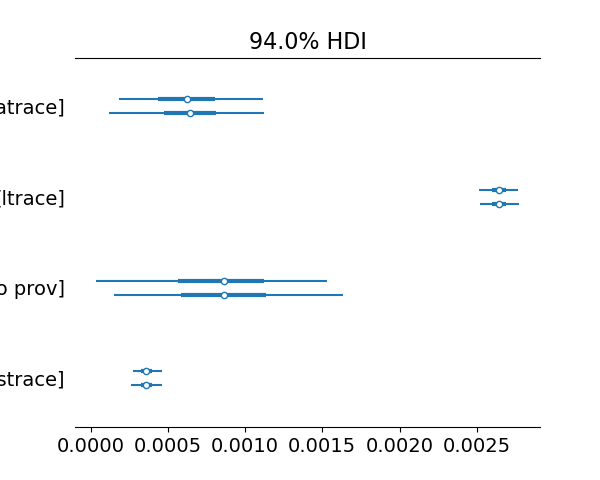
  1. Is this a problem for regression? I don’t get any warnings, but the posterior for overhead_per_line["no logging"] is quite wide (see the third row in the following figure).

overhead_per_line

  1. Is there a way to specify the following model which switches off between including and not including overhead_per_line[logging_engine]?
runtime ~
  Normal(inherent_runtime, runtime_std)
  if logging_engine == "no logging" else
  Normal(inherent_runtime + num_ops * overhead_per_line[logging_engine], runtime_std)

Full model: Partially pooled linear regression when x[0] == 0 for all instances where x[1] == "specific-class" · GitHub

1 Like