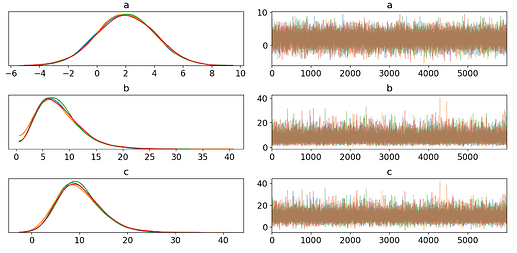
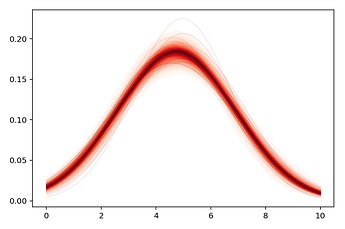
So, recently I was wondering whether it would be possible to probabilistically represent a whole distribution out of the parameters that a Pymc3 model fits.
For example, using the following code, I can calculate the mean, \mu, as well as the standard deviation, \sigma, from a normally generated dataset easily:
## Data generated from a normal distribution, with mean 5 and std 2
normal_data = np.random.normal(5,2,100)
with pm.Model() as model:
# Priors (a bit narrow only for the sampler's convenience)
mu_sigma = pm.HalfNormal('mu_sigma', sd = 10)
mu = pm.Normal('mu', mu = np.mean(normal_data), sigma = mu_sigma)
sigma = pm.Uniform('sigma', lower = 0.001, upper = 10)
# Likelihood
likelihood = pm.Normal('likelihood', mu = mu, sigma = sigma, observed = normal_data)
# Distribution that I would like to recover
recovered_normal = pm.Normal('recovered_normal', mu, sigma) # I am not sure what this accomplishes
trace = pm.sample(cores=4, draws=2000, tune=2000, target_accept=0.95)
Using pm.summary(), I would like to see that recovered_normal has the same values as the 2 fitted priors composing it.
However, the estimated \mu and \sigma do not seem to align (though they’re close) with recovered_normal's variables, which is what I was aiming for.
In the end, how could I create a variable object that perfectly draws on variables fit by a model? The reason I am asking this is because that would allow for for convolution with fitted distributions, since math operations already work with regular pm.Normal()'s (or any other priors) if put in a pm.Deterministic().
Any advice would be dearly appreciated.