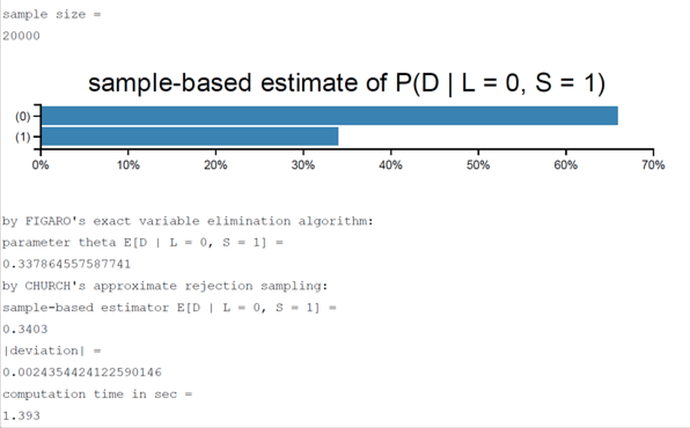
I successfully made the student BN example with PYMC3. It seems it gives the general answer correctly.

Is there an easy way to make a query for observation like {L=L0, S= S1}
The code and CPDs are as follow:
D = np.array([0.6, 0.4])
I = np.array([0.7, 0.3])
G = np.array([[[0.3, 0.4, 0.3],
[0.05, 0.25, 0.7]],
[[0.9, 0.08, 0.02],
[0.5, 0.3, 0.2]]])
S = np.array([[0.95, 0.05],
[0.2, 0.8]])
L = np.array([[0.1, 0.9],
[0.4, 0.6],
[0.99, 0.01]])
with pm.Model() as model:
I_ = pm.Categorical('I', p=I)
D_ = pm.Categorical('D', p=D)
G_prob = theano.shared(G)
G_0 = G_prob[I_, D_]
G_ = pm.Categorical('G', p=G_0)
S_prob = theano.shared(S)
S_0 = S_prob[I_]
L_prob = theano.shared(L)
L_0 = L_prob[G_]
L_ = pm.Categorical('L', p=L_0)
with model:
trace = pm.sample(20000)
Thanks