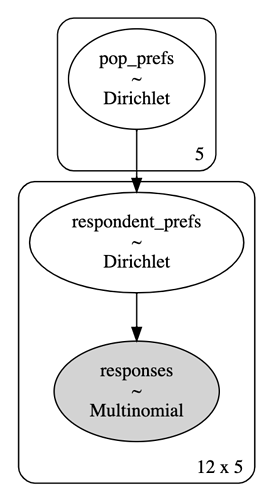
I am trying to use an HGLM to model responses to a preference test. Each survey question shows the user two versions of the same image: one filtered by algorithm A v.s. one filtered by algorithm B. The possible responses are:
- Strongly Prefer A
- Prefer A
- No Preference
- Prefer B
- Strongly Prefer B
… except users aren’t actually told which is A or B.
I am trying to create a model that will, to the extent possible, characterise the preferences of all people, not just those who responded. It must be resilient to different people answering a different number of questions.
Here’s my code, and some data from my trial survey…
# Data from survey respondents.
df = pd.DataFrame(
columns = ['STRONG_A', 'A', 'NO_PREF', 'B','STRONG_B'],
data = [
[14, 7, 4, 11, 42],
[3, 2, 0, 4, 13],
[1, 3, 16, 17, 15],
[2, 4, 5, 14, 7],
[1, 5, 2, 7, 20],
[7, 1, 1, 7, 14],
[5, 9, 16, 10, 26],
[9, 0, 7, 12, 22],
[6, 2, 1, 4, 28],
[0, 2, 8, 11, 10],
[0, 10, 3, 11, 26],
[1, 10, 5, 22, 20],
],
)
# Number of responses from each person.
df_n = df['STRONG_A'] + df['A'] + df['NO_PREF'] + df['B'] + df['STRONG_B']
n_options = 5
n_respondents = len(df)
with pm.Model() as model:
# The preferences of all people, not just those who responded.
pop_prefs = pm.Dirichlet(
"pop_prefs",
a=np.ones(n_options),
shape=n_options,
);
# The preferences of each survey respondent.
respondent_prefs = pm.Dirichlet(
"respondent_prefs",
a=pop_prefs,
shape=(n_respondents, n_options),
);
responses = pm.Multinomial(
"responses",
n=df_n,
p=respondent_prefs,
shape=(n_respondents,n_options),
observed=df
)
trace = pm.sample(
10000,
tune=5000,
return_inferencedata=True
)
az.plot_trace(trace)
az.summary(trace, var_names=["pop_prefs"])
Here are the results…
My expectation was that pop_prefs would characterise the preferences of the population, whilst respondent_prefs would account for variation from the “typical” person (loosely speaking). Running the model gave an expected probability of responding STRONGLY_PREFER_B of 0.264. If we take the average from the raw data, it’s .446. At first I assumed the discrepancy was due to regularization from a flat prior, but if I copy paste the data three times to simulate having more evidence, the result remains the same except with a narrower confidence interval, which suggests I’m misunderstanding something. The same happens with synthetic data generated from a distribution.
What am I doing wrong? I’m just an engineer who is trying to teach themselves Bayesian modelling, and I would greatly appreciate any guidance. I’ve read Statistical Rethinking twice now ![]() Thank you!
Thank you!