I’m trying to make a model with compound Poisson distribution. It’s pdf is:
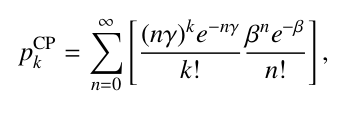
I made the logp and random variates functions but not sure how to implement them as a distribution class. Does anyone have an experience?
I’m trying to make a model with compound Poisson distribution. It’s pdf is:
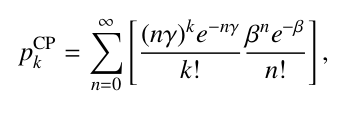
I made the logp and random variates functions but not sure how to implement them as a distribution class. Does anyone have an experience?
Welcome!
It seems like you are missing a dist() method? And I’m not sure what your CP method is. Have you ready up about implementing PYMC distributions here?
Generally it will be easier to use pm.CustomDist, rather than implementing all the machinery of distribution class.
Also the import theano.tensor line is worrying to me. It’s strongly recommended you use the latest version of PyMC and pytensor.
CP function is just the pdf of my custom compound Poisson dist. I gave it in beginning. I implemented a negative binomial distribution to check my code again but there is the same problem.
if I use pymc.CustomDist the error pops up:
NotImplementedError: Logprob method not implemented for CustomDist_CompoundPoisson_rv{0, (0, 0), floatX, False}
You need to provide a logp function that returns the logp using exclusively Pytensor operations. Can you show the code you tried?
I think because the log probability of the compound Poisson pdf for zero gamma and lambda will be log(0) it gives
If you can, please paste your code as text rather than images.
What version of PyMC are you using?
yes sure. Below is the code. I made some changes to be better readable. The pdf is from the formula I gave in beginning of the discussion. I just took log of the pdf by theano to make a log probability because I didn’t know the analytic form of the log probability of the compound Poisson dist. mu and var are the mean and variance of the data.
The version of pymc is 5.10.4.
import pymc
import mpmath as mp
import theano as tt
def logCompoundPoisson(mu, var, k):
gamma = (var - mu) / mu
beta = mp.power(mu, 2) / (var - mu)
cp = mp.nsum(lambda n: (mp.power((n * gamma), k) * mp.exp(-n * gamma)
* mp.power(beta, n) * mp.exp(-beta)) /
(mp.gamma(k + 1) * mp.gamma(n + 1)),
[0, mp.inf])
return tt.log(cp)
with pymc.Model() as model:
mu = pymc.Gamma("mu", 5,1)
var = pymc.Gamma("var", 10, 1)
pymc.CustomDist("CompoundPoisson", mu, var, logp= logCompoundPoisson, observed= data)
trace3 = pymc.sample_smc(400, random_seed=42)
PyMC should use PyTensor operations not theano. Basically you can replace theano.tensor by pytensor.tensor and use the same methods.
However your logp must be written with PyTensor constructs, not numpy/mpmath. You can wrap these in PyTensor Ops if you wish to, but that may be suboptimal compared to just using PyTensor constructs: Using a “black box” likelihood function (numpy) — PyMC example gallery
We are updating that example, so if you want to check the upcoming version: Update blackbox likelihood example by ricardoV94 · Pull Request #631 · pymc-devs/pymc-examples · GitHub
I used PyTensor Ops as below.
import pymc
import mpmath as mp
import pytensor.tensor as pt
def logCompoundPoisson(input_vector, k):
mu, var = input_vector
gamma = (var - mu) / mu
beta = mp.power(mu, 2) / (var - mu)
cp = mp.nsum(lambda n: (mp.power((n * gamma), k) * mp.exp(-n * gamma)
* mp.power(beta, n) * mp.exp(-beta)) /
(mp.gamma(k + 1) * mp.gamma(n + 1)),
[0, mp.inf])
return mp.log(cp)
# define a pytensor Op for our log probability function
class LogProbability(pt.Op):
itypes = [pt.dvector] # expects a vector of parameter values when called
otypes = [pt.dscalar] # outputs a single scalar value (the log probability)
def __init__(self, logpro, k):
self.likelihood = logpro
self.k = k
def perform(self, node, inputs, outputs):
(input_vector,) = inputs
logp = self.likelihood(input_vector, self.k)
outputs[0][0] = np.array(logp)
k = np.arange(0,50)
logp = LogProbability(logCompoundPoisson, k)
# use PyMC to sampler from log-probability
with pm.Model():
# uniform priors on m and c
mu = pm.Gamma("mu", 1, 1)
var = pm.Gamma("var", 10, 1)
# convert mu and var to a tensor vector
input_vector = pt.as_tensor_variable([mu, var])
# use a Potential to "call" the Op and include it in the logp computation
pm.Potential("likelihood", logp(input_vector))
idata = pm.sample(300, tune=1000)
but the following error pops up:
Are you sure you need mpmath. I would first try just vanilla pytensor sum. No custom Ops or anything like that
I used it for its nsum to do the summation from n=0 to inf. How can I replace it with pytensor sum?
Is there a way to implement the compound Poisson distribution in pymc distribution list, because it is one of the widely used discrete distributions?