Problems with a Joint Species Distribution Model (jdsm): Implementing a multiplicative Gamma Prior

[C.A_Mallon]

TLDR

I am trying to implement a multiplicative gamma prior into a multivariate, hierarchical model. I’d be grateful for someone to double check this to make sure I am technically implementing the prior in the correct way. Advice on anything else in the model that catches your eye is also welcome! I’m also writing this as a longer, more extensive post because I haven’t seen this family of models being used in python or pymc, and perhaps others will find this useful. And also for anythone willing to help, so that they understand the whole model.

The Model

I am setting up a joint species distribution model (jsdm). I’ve read the book Joint Species Distribution Modelling, With Applications in R by Ovaskainen and Abrego, which details the theory and use (in R) of these models. If you are interested their R package for jdms, called HMSC, please see their website https://www.helsinki.fi/en/researchgroups/statistical-ecology/software/hmsc. I’m now trying to set up these models in pymc to really learn how they work and also for more modelling flexibility in the future. I’ve made the post a bit extensive, so anyone else using a similar model can hopefully learn from this, as well as to provide an in depth explanation of the model. These models are complex. They are multivariate and hierarchical. They have fixed effects and random effects, where the random effects are modeled using a latent variable approach. And I use non-centered parameterization to achieve efficient sampling. Overall, I guess one could call a jdsm a “hierarchical multivariate generalized linear mixed-effects model with latent variables.” This family of models is used in ecology to achieve at least two primary goals. First, these models aim to understand how phenotypic and genetic information influences the niche of a species. Thus, environmental covariates, as well as phenotypic and/or genetic variation, can be included as fixed effects. Second, these models aim quantify species co-occurences, where a latent variable approach is employed to capture residual variance (random effects) across different locations. The purpose of this post primarily deals with the latter goal, to model species co-occurences.

The latter goal is achieved by modelling the residual error of the model (i.e., the randon effect) using latent variables. Latent factors are assigned at the level of the location (think per plot of land, postcode, or individual), representing shared environmental or spatial effects. Each species has species-specific loadings on these latent factors, and these loadings capture how strongly a species is influenced by each latent factor. By examining the covariance of these latent loadings across species and locations, patterns of species co-occurrence can be quantified.

I think I’ve got most of the modelled figured out. A simpler version of the model, without random effects for instance, samples well and shows convergence among chains. More complex versions of the model, where random effects are added, display divergences and sampling problems. The most complicated part of the model, contained into the random effects, is the prior on the latent species loadings. As I ask in more detail later in this post, Could someone please take a look at the model to see if I have set up the prior, as it has been described in the book by Ovaskainen and Abrego.

Note again that the model theory, equations, and notation comes from the book Joint Species Distribution Modelling, With Applications in R by Ovaskainen and Abrego. These methods are widely employed in papers from Ovaskainen statistical ecology lab.

The Linear Predictor

Here’s what the model looks like:

L_{ij} = L_{ij}^F + L_{ij}^R

where L is the linear predictor of species j in location i. It is the sum of both a fixed and random effect.

In matrix notation the model looks like this:

\mathbf{L} = \mathbf{L}^F + \mathbf{L}^R, \quad \text{where } \mathbf{L}^F = \mathbf{X} \mathbf{B} \text{ and } \mathbf{L}^R = \mathbf{H} \mathbf{\Lambda}.

The fixed effects represent the contribution of environmental covariates, \mathbf{X}, to species responses modeled through a matrix of coefficients, \mathbf{B}. The random effects capture structured residual variation using latent variables, \mathbf{H}, and species-specific loadings, \mathbf{\Lambda}, which account for species co-occurrence patterns. The response variable in my case is a binary matrix, representing the presence or absence of species across different locations.

Variables and Parameters

Fixed effects are modelled as:

L_{ij}^F = \sum_{k=1}^{n_c} x_{ik} \beta_{kj}

where L_{ij}^F are the sum of the product of environmental covariates and their coefficients. x is the value of environmental covariate k at location i. And \beta is the response of species j to environmental covariate k. n_c is the number of environmental covariates, including the intercept.

Random effects are modelled as:

L_{ij}^R = \sum_{h=1}^{n_f} \eta_{ih} \lambda_{hj}

where L_{ij}^R is the sum of latent factors and loadings. \eta_{ih} is latent factor h of location i. And \lambda_{hj} is the loading of species j on latent factor h. Notice that the latent factor is site-specific. This means that each location, we will create a latent factor \eta. Factor loadings/weights, \lambda are then estimated for each species.

This is less important, but if you’re curious, in order to assess correlations between species pairs, we essentially sum up the product of species’ pairs loadings across all latent variables (the latent variables being site specific). So those species that consistently have higher loadings on latent variables across all sites, will have higher covariances and eventually stronger co-correlations. Here is the formula for calculating species’ pairs covariance:

\text{Cov}\left[L_{i_1,j_1}^R, L_{i_2,j_2}^R\right] = \sum_{h=1}^{nf} \lambda_{h j_1} \lambda_{h j_2} \delta_{i_1 i_2}

\delta is the Kronecker delta, where the value is 1 if i_1 = i_2. The value is 0 if they (i.e., sites/infants) are not equal.

Model Assumptions (i.e, Priors)

Prior for Fixed Effects \beta

The fixed effect coefficients, \beta, are modeled using a non-centered parameterization with a multivariate normal (MVN) prior. The prior for \beta is constructed as follows:

Hyperpriors

1. Mean vector \mu_{\beta}:
   \mu_{\beta} \sim \mathcal{N}(0, 2), where each element of \mu_{\beta} represents the average species response to the covariates. I am using a std. dev. of 2, but it could of course be a different value. The length of this vector is equal to the number of environmental covariates in the model, plus the intercept.

2. Covariance structure:

   • Standard deviations \sigma_{\beta} are modeled with a Half-Cauchy distribution:
     \sigma_{\beta} \sim \text{Half-Cauchy}(2).
   • Covariances and variances are modelled with the LKJ prior with \eta = 1.
   • I am actually modelling the variance-covariance structure differently than Ovaskainen and Abrego. They use the inverse-Wishart. But as I have learned the pymc NUTS sampler works better with the LKJ prior on var-covar matricies.

Non-Centered Parameterization

I previously was not using non-centered parameterization, but I was getting a lot of divergences. Following this post https://www.pymc.io/projects/examples/en/latest/generalized_linear_models/multilevel_modeling.html, I then employed non-centered parameterization and got far fewer divergences. (Although I do wonder exactly what the trade-off of this method is. I guess we are essentially forcing the model to better explore the prior distribution of the LKJ prior. But to what extent is this realistic and you don’t end up with extreme species niches? Perhaps better for another discussion.)

The fixed effects \beta are expressed in terms of a standard normal latent variable z and the Cholesky factor of the covariance matrix L_{\beta}:

\beta = \mu_{\beta} + z \cdot L_{\beta}^{T}

where z \sim \mathcal{N}(0, 1).

All in all, we are essentially drawing all species-level \beta values from a common, multivariate distribution. This allows a regularization or “borrowing” of information, where the likelihood of the MVN is better informed by more common species, allowing the \beta values for less common species are shrunk towards the community mean. This increases the confidence we have for the \beta estimations of rare species to environmental covariates and also it allows one to include a large number rare species in the model.

Latent Factor Prior

The prior on latent factors \eta_{ih} on each latent factor h, in each location i, are independent and follow a standard normal distribution:

\eta_{ih} \sim \mathcal{N}(0, 1)

Species Loadings Prior: Multiplicative Gamma Shrinking Process

Here’s where things really heat up.
In order (i) ensure species loadings for each latent factor are not overfit and (ii) ensure that later latent factors explain less of the variation, the prior introduces two levels of shrinkage:

1. Local shrinkage (\Phi): Captures species-specific variability. This is modeled by a matrix \Phi with dimensions n_f \times n_s, where n_f is the number of latent factors, and n_s is the number of species.
2. Global shrinkage (\delta): Captures shared variability across species. This is modeled by a vector \delta of length n_f, with increasing shrinkage applied to higher latent factors. When setting up the model in PyMC, this technically means different parameter values are assigned to the species loading prior, depending on whether the loading is applied to the first or later latent factors

According to Ovaskainen and Abrego (2020, see chapter 8) and based on Bhattacharya and Dunson (2011), the prior density for \Lambda, \Phi, and \delta is given by:

p(\Lambda, \Phi, \delta) = p(\Lambda \mid \Phi, \delta)p(\Phi)p(\delta)

with components defined as:

1. Species loadings (\lambda_{ij}):

   \lambda_{ij} \mid \phi_{hj}, \delta \sim \mathcal{N} \left( 0, \frac{1}{\phi_{hj} \cdot \tau_h} \right), \quad \tau_h = \prod_{l=1}^h \delta_l

   Each element of \Lambda is normally distributed with a variance inversely proportional to the product of local (\phi_{hj}) and global (\tau_h) shrinkage terms.

2. Local shrinkage (\phi_{hj}):

   \phi_{hj} \sim \text{Gamma} \left( \frac{u}{2}, \frac{u}{2} \right)

   The parameter u controls the strength of local shrinkage for species-specific loadings.

3. Global shrinkage (\delta_h):

   \delta_1 \sim \text{Gamma}(a_1, b_1), \quad \delta_h \sim \text{Gamma}(a_2, b_2) \quad \text{for } h \geq 2
   • The first global shrinkage parameter (\delta_1) has its own Gamma distribution.
   • Subsequent global shrinkage parameters (\delta_h, for h \geq 2) are drawn from a different Gamma distribution.
   • As alluded to above, this distinction ensures that the prior allows greater flexibility for the first latent factor, which typically captures most of the variability.

4. Values used by Ovaskainen and Abrego (2020).

   • u = 3, \quad a = (50, 50), \quad b = (1, 1). They mention that users of the model should choose \quad a = (50, 50) carefully. Similar to what they did in their book, I have performed simulation experiments using parameter values: \quad a = (50, 50) , \quad a = (50, 3), \quad a = (3, 50), and \quad a = (3, 50).

As explained by Ovaskainen and Abrego (2020), “Thus, the prior of the species loadings is normally distributed, with a mean of zero and precision (inverse of variance) modeled as a product of gamma-distributed random variables.”

My Questions

Below I have done some parameter recovery experiments where I simulate data, using the model structure described above, with known parameter values. I train the model using pymc on that data to see if it can recover the parameters back. What I first see from the traces is that everything from the fixed effects (mu_beta, LKJ variance-covariance) is well sampled. However, the random effects are poorly sampled. The \lambda parameters are very poorly sampled, and the chains are highly divergent. But, as \lambda is a function of \phi and \delta, the problem may lie with one of these parameters. \delta appears very well sampled. \phi is not well sampled.

The problem may thus be the sampling of the \phi parameter. In some cases, \phi appears well sampled and all four chains converge. In other cases, one of the chains is highly divergent to the other three. In these cases, it seems it might be more difficult to sample \phi when its value is close to zero.

Therefore, if someone has time to look, would you, first, be able to let me know if I have implemented the prior on species loadings as I describe it in the text above? This goes for \phi, \delta, and \lambda , which all compose the species loadings prior. Note for \phi I have tried a four sets of values: \quad a = (50, 50),\quad a = (3, 50),\quad a = (50, 3),\quad a = (3, 3). The values that give the best results, \quad a = (3, 3) are shown below. The problem with \phi is exacerbated with the other values, most extreme with \quad a = (50, 50). Second, if I have indeed implemented everything correctly, would you have any ideas on how to better sample \phi? And, third, might you have any ideas other ideas on how to improve the model in general?

References

Ovaskainen, O., & Abrego, N. (2020). Joint Species Distribution Modelling, With Applications in R. Cambridge University Press. https://doi.org/10.1017/9781108561138
Bhattacharya, A., & Dunson, D. B. (2011). Sparse Bayesian infinite factor models. Biometrika, 98(2), 291–306. https://doi.org/10.1093/biomet/asr013

Define Model in PYMC

import pymc as pm
import numpy as np
from pymc.model_graph import model_to_graphviz
from IPython.display import display

# Set a random seed for reproducibility
rng = np.random.default_rng(seed=42)

h = 3 # latent factors
j = 30 # species
i = 100 # locations
k = 5 # covariates (including intercept)

# Create X_data with the first column as ones (intercept) and the rest as continuous values
# this is used later for the parameter recover experiment
X_data = np.hstack([np.ones((i, 1)), rng.uniform(0, 1, size=(i, k - 1))])

# define model with proper dimensions for Y
y_placeholder = np.zeros((i, j))
                   

with pm.Model() as jdsm_model:
     
    # declaring the data     
    X = pm.Data("X", X_data)
    y_sim = pm.Data("y_sim", y_placeholder)  # placeholder for observed data

    
   # Hyperpriors for the shared covariance structure of beta (species responses to covariates)
    mu_beta = pm.Normal('mu_beta', mu=0, sigma=2, shape=k)  # Mean of MVN for beta

    # Prior stddev in intercepts & slopes (variation across counties) using Half-Cauchy
    sd_dist = pm.HalfCauchy.dist(beta=2)

    # LKJ prior for the Cholesky factor of the covariance matrix
    L_beta_cov, L_beta_corr, L_beta_sd = pm.LKJCholeskyCov(
        'L_beta', n=k, eta=1, sd_dist=sd_dist, compute_corr=True)

    # Non-centered reparameterization
    z = pm.Normal('z', mu=0, sigma=1, shape=(j, k))  # Standard normal latent variable
    beta = pm.Deterministic('beta', mu_beta + pm.math.dot(z, L_beta_cov.T))  # Non-centered beta

    # Latent site-specific loadings (η)
    eta = pm.Normal('eta', mu=0, sigma=1, shape=(i, h))

    # Multiplicative Gamma Process Shrinking Prior for species loadings (Λ)
    # Global shrinkage parameters (δ)
    a = [3, 3]
    b = [1, 1]
    
    # Create alpha and beta arrays, for h number of latent factors
    alpha_values = np.array([a[0]] + [a[1]] * (h - 1))
    beta_values = np.array([b[0]] + [b[1]] * (h - 1))

    # pass params to delta
    delta = pm.Gamma('delta', alpha=alpha_values, beta=beta_values, shape=h)
    
    # Local shrinkage parameters (Φ)
    v = 3
    phi = pm.Gamma('phi', alpha=v / 2, beta=v / 2, shape=(h, j))

    # Species loadings on latent factors (Λ)
    Lambda = pm.Normal('Lambda', mu=0, sigma=1 / pm.math.sqrt(phi * delta[:, None]), shape=(h, j))

    # Random effects modeled through latent variable approach
    LR = pm.math.dot(eta, Lambda)

    # Fixed effects modeled through the linear predictor
    LF = pm.math.dot(X, beta.T)

    # Combined linear predictor: fixed effects + random effects
    linear_predictor = pm.Deterministic('linear_predictor', LF + LR)

    # Logit link function to transform linear predictor to the probability space (0, 1)
    p = pm.Deterministic('p', pm.math.sigmoid(linear_predictor))

    # Likelihood for simulated data (without observed Y data)
    Y_pred = pm.Bernoulli('Y_obs', p=p, observed=y_sim)
    
# The DAG
model_graph = model_to_graphviz(jdsm_model)
model_graph.format = 'png'
model_graph.render("dag_output", cleanup=True)
Image(filename="dag_output.png")

Simulate Some Data

# true parameter values
true_mu_beta = np.zeros(k)
true_L_beta_cov = np.eye(k)  # Identity covariance matrix
true_eta = rng.normal(0, 1, size=(i, h))
true_Lambda = rng.normal(0, 1, size=(h, j))
true_beta = rng.multivariate_normal(true_mu_beta, true_L_beta_cov, size=j)

# Simulate outcomes
LR = np.dot(true_eta, true_Lambda)  # Random effects
LF = np.dot(X_data, true_beta.T)  # Fixed effects
linear_predictor = LF + LR
p = 1 / (1 + np.exp(-linear_predictor))  # Sigmoid link
Y_sim = rng.binomial(1, p)  # Binary outcomes

Sample/Fit the Model

with jdsm_model:
    pm.set_data({"y_sim": Y_sim})  # Use simulated data as observed outcomes
    trace = pm.sample(4000, tune=2000, chains=4, target_accept=0.90)

Examine How the Model Sampled

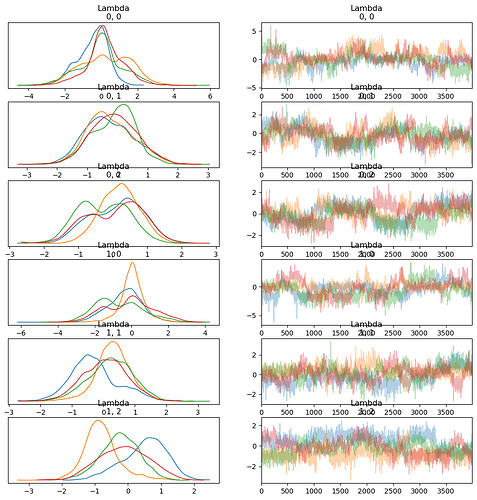
As I explained previously it seems parameters from the fixed effects are well sampled. However, the random effects are poorly sampled. The problem may be with the sampling of the \phi parameter. In some cases, \phi appears well sampled and all four chains converge. In other cases, one of the chains is highly divergent to the other three. In these cases, it seems it might be more difficult to sample \phi when its value is close to zero. \delta seems well sampled. \lambda is not well sampled.

# plot traces for params of interest
az.plot_trace(trace, var_names=["mu_beta"])
az.plot_trace(trace, var_names=["L_beta"],  coords={"L_beta_dim_0": [0, 1, 2, 3, 4, 5]},  compact=False)
az.plot_trace(trace, var_names=["Lambda"], coords={"Lambda_dim_0": [0, 1], "Lambda_dim_1": [0,1,2]}, compact=False)
az.plot_trace(trace, var_names=["delta"], compact=False)
az.plot_trace(trace, var_names=["phi"], coords={"phi_dim_0": [0,1], "phi_dim_1": [0,1,2,3,4,5,6]}, compact=False)

#    (chain: 4, draw: 4000, L_beta_dim_0: 15,
#                             L_beta_corr_dim_0: 5, L_beta_corr_dim_1: 5,
#                             L_beta_stds_dim_0: 5, Lambda_dim_0: 3,
#                             Lambda_dim_1: 30, beta_dim_0: 30, beta_dim_1: 5,
#                             delta_dim_0: 3, eta_dim_0: 100, eta_dim_1: 3,
#                             linear_predictor_dim_0: 100,
#                             linear_predictor_dim_1: 30, mu_beta_dim_0: 5,
#                             p_dim_0: 100, p_dim_1: 30, phi_dim_0: 3,
#                             phi_dim_1: 30, z_dim_0: 30, z_dim_1: 5)

Recovering \beta

This suggests I should increase the sd of the scaling factor z, as the range of my recovered \beta values is about from -2 to 2, and not spanning the range of true \beta values.

import matplotlib.pyplot as plt
# Posterior estimates
posterior_beta = trace.posterior['beta'].mean(dim=('chain', 'draw'))

# Plot comparison
plt.plot(true_beta, posterior_beta, 'o')
plt.plot(true_beta, true_beta, 'k--', label='True = Recovered')
plt.xlabel("True Beta")
plt.ylabel("Recovered Beta")
plt.legend()
plt.title("Parameter Recovery: Beta")
plt.show()

Recovering \lambda

As is visible, the \lambda recovery is way off. I also don’t understand why the recovered values are mostly around 0.

posterior_Lambda = trace.posterior['Lambda'].mean(dim=('chain', 'draw')).values

# Compare true vs. recovered Lambda for each latent factor
for h in range(true_Lambda.shape[0]):  # Iterate over latent factors
    plt.figure(figsize=(6, 6))
    plt.plot(true_Lambda[h, :], posterior_Lambda[h, :], 'o', label=f'Factor {h+1}')
    plt.plot(true_Lambda[h, :], true_Lambda[h, :], 'k--', label='True')  # Line of perfect recovery
    plt.xlabel(f"True Lambda (Factor {h+1})")
    plt.ylabel(f"Recovered Lambda (Factor {h+1})")
    plt.legend()
    plt.title(f"Parameter Recovery: Lambda (Factor {h+1})")
    plt.show()

[fonnesbeck]

Thanks for such a thorough description of the problem! I like a good ecology example.

A question I have is regarding what you call “fixed effects”. If each species has its own beta, which is drawn from a distribution with hyperparameters, then it seems to me that you are dealing with another random effect (keeping in mind that fixed/random effects are loaded terms that mean different things to different people). So if you combine this additively with another random effect by species, then you may be running into an identifiability problem(?) where species-level variation can be assigned to either random effect. You could check this by making beta be constant across species (which is what I would regard as a fixed effect) and see if that fixes the problem with your Lambdas.

Also, keep in mind that the gamma distribution in PyMC is parameterized by a rate parameter (beta) whereas the gamma in R is (typically, but not always) parameterized by a scale parameter (sigma). You should check whether HMSC uses this parameterization.

Hope some of this helps!

[C.A_Mallon]

@fonnesbeck Thank you so much for your quick reply! Actually, I hadn’t even thought of the identifyibility problem. I also don’t think I’ve seen this problem explicitly discussed in the ecological literature. It is typically recommended to start with simpler models, with a few covariates and a limited number of latent factors, and then to perform cross-validation on your model to examine problems related to overfitting. In doing so, I guess one reduced the competition for variance between each random effect. But I think making \beta constant across species is a great tip to examine this problem! So I’ll do so and report back.

And as for parameterizing a gamma distribution in pymc vs R, actually I can’t believe I overlooked this, but I think rgamma() deals with shape and rate, not mean and variance. So i’ll check this out too.

Thank you again! And I’ll add to this thread soon!

[cluhmann]

@C.A_Mallon

I think rgamma() deals with shape and rate, not mean and variance

rgamma() uses shape and scale, PyMC uses shape and rate. The wikipedia page for the gamma distribution covers these different parameterizations. PyMC also has a parameterization that uses the mean and “alternative scale” (see here).

[C.A_Mallon]

Thank you for the clarification!

[fonnesbeck]

Both R and PyMC can be parameterized either way, but the defaults are different.

[fonnesbeck]

@C.A_Mallon

It is typically recommended to start with simpler models, with a few covariates and a limited number of latent factors, and then to perform cross-validation on your model to examine problems related to overfitting.

You can use loo from ArviZ with PyMC models to perform approximate leave-one-out cross validation without having to explicitly run N models.