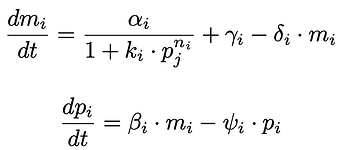Pymc inference for a high dimensional ODE system

Questions version agnostic
1

Hello Pymc Community!

I am trying to obtain a ground truth posterior distribution over the parameters of a ≥10 parameter ODE model for the Repressilator system (21 parameters) as shown below:

Screenshot 2025-02-07 at 18.52.16
Screenshot 2025-02-07 at 18.52.16756×330 9.64 KB

I can make some assumptions to reduce the parameters to obtain simpler models (3, 6, 9, 12, 15, 21 parameters).

I have used pymc with the DE Metropolis Z sampler as the following snippet of minimal code shows and have gotten satisfactory ground truth distributions for the 3, 6 and 9 parameter versions of the ODE system:

@njit
def Rep_model_odeint(X, t, theta):
    # unpack parameters
    m1, p1, m2, p2, m3, p3 = X
    b1, b2, b3 = theta

    dm1dt = -m1 + (1000.0 / (1.0  + (p2)**2.0)) + 1.0
    dp1dt = - b1 * (p1 - m1)    
    
    dm2dt = -m2 + (1000.0 / (1.0 + (p3)**2.0)) + 1.0
    dp2dt = - b2 * (p2 - m2)    

    dm3dt = -m3 + (1000.0 / (1.0 + (p1)**2.0)) + 1.0
    dp3dt = -b3 *(p3 - m3)    

    return [dm1dt, dp1dt, dm2dt, dp2dt, dm3dt, dp3dt]

# # decorator with input and output types a Pytensor double float tensors
@as_op(itypes=[pt.dvector], otypes=[pt.dmatrix])
def pytensor_forward_model_matrix_Rep_model(theta):
    return odeint(func=Rep_model_odeint, y0 = initial_conditions, t = t, args=(theta,),)

initial_conditions = np.array([0.0, 2.0, 0.0, 1.0, 0.0, 3.0])
num_timesteps = 50  # Number of time steps for simulation
t = np.linspace(0, 40, num_timesteps) #Range of time of simulation
sigma = 0.5
# 
with pm.Model() as Rep_model:
    # Priors
    # sigma = pm.Uniform("sigma", 0, 2)
    b1 = pm.Uniform("b1", 0, 10)
    b2 = pm.Uniform("b2", 0, 10)
    b3 = pm.Uniform("b3", 0, 10)

    # Ode solution function
    ode_solution = pytensor_forward_model_matrix_Rep_model(
        pm.math.stack([b1, b2, b3]), 
    )
    # Likelihood
    pm.Normal("Y_obs", mu=ode_solution, sigma=sigma, observed=yobs)

vars_list = list(Rep_model.values_to_rvs.keys())[:-1]
sampler = "DEMetropolisZ"
draws = tune = 5000
with Rep_model:
    trace_DEMZ = pm.sample(step=[pm.DEMetropolisZ(vars_list)], tune=tune, draws=draws)

However, for the more complex versions, I have been struggling to get the ground truth estimates. Even with running this for almost a day on an HPC cluster, I get warning messages saying that the r hat is >1 or ESS is too small.

Can anyone suggest as to what all I can tinker with in order to get these estimates? Like perhaps changing proposal variance etc.?

I have already tried sampling > 10 million points, and every other sampler is extremely slower compared to the DEMZ sampler.

Any help would be highly appreciated as I am near the end of my project.

2

The as_op decorator seems unnecessary. You can use pytensor operations, and if you want to exploit numba for the the whole logp (and automatically dlogp because you didn’t use as_op), pass compile_kwargs=dict(backend="NUMBA") to pm.sample

For the intricacies of ODEs @aseyboldt may have some hints

1 Like
3

Thanks alot for your reply!

Removing the as_op decorator gives me errors and passing compile_kwargs=dict(backend="NUMBA") to pm.sample, has no appreciable effects on the time of convergence.

For the >=12 parameter versions of the model, the algorithm does not converge even after running for 2 days. Is there something else I can do?

4

I suspect the unpacking from the vector? Just pass the variables separately. Otherwise there’s nothing I see that could fail

5

Ahh you have an odeint there, what library is that?

There’s sunode for PyMC models that doesn’t need any as_op for sure