I am new to learning MCMC and I have a nonlinear model like this:
Takano_model_1 = pm.Model()
with Takano_model_1:
## Priors
A_f = pm.Bound(pm.Normal, lower=0.0)(“A_f”,mu = 3.8671, sigma = 3.867110)
A_r = pm.Bound(pm.Normal, lower=0.0)(“A_r”,mu = 1.1635, sigma = 1.163510)
A_CO2 = pm.Bound(pm.Normal, lower=0.0)(“A_CO2”,mu = 2.5027, sigma = 2.502710)
A_H2O = pm.Bound(pm.Normal, lower=0.0)(“A_H2O”,mu = 5.5128, sigma = 5.512810)
### Activation energy (unit:J/mol)
Ea_f = pm.Bound(pm.Normal, lower=0.0)(“Ea_f”,mu = 2.2768, sigma = 2.276810)
Ea_r = pm.Bound(pm.Normal, lower=0.0)(“Ea_r”,mu = 1.1445, sigma = 1.144510)
Ea_CO2 = pm.Bound(pm.Normal, upper=0.0)(“Ea_CO2”,mu = -3.2333, sigma = 3.233310)
Ea_H2O = pm.Bound(pm.Normal, lower=0.0)(“Ea_H2O”,mu = 7.7608, sigma = 7.760810)
sigma = pm.HalfNormal(‘sigma’,sd = 0.0003)k_f = A_f * 1.0E02 * (math.e ** (- Ea_f * 1.0E04 / R / T_Bottom)) k_r = A_r * 1.0E08 * (math.e ** (- Ea_r * 1.0E05 / R / T_Bottom)) K_CO2 = A_CO2 * 1.0E-05 * (math.e ** (- Ea_CO2 * 1.0E04 / R / T_Bottom)) K_H2O = A_H2O * 1.0E07 * (math.e ** (- Ea_H2O * 1.0E04 / R / T_Bottom)) r_CH4_obs = k_f * (K_CO2 * p_CO2_in * p_H2_in ** 0.5) / ((1 + K_CO2 * p_CO2_in) ** 2) - k_r * (K_H2O * p_CH4_in ** 2 * p_H2O_in) / ((1 + K_H2O ** 2 * p_H2O_in) ** 2) ##Likehood function r_CH4_likehood = pm.Normal('r_CH4_likehood',mu = r_CH4_obs, sd = sigma, observed = r0_CH4)
Due to the conditions of the chemical equation, bound is applied to the prior distribution.
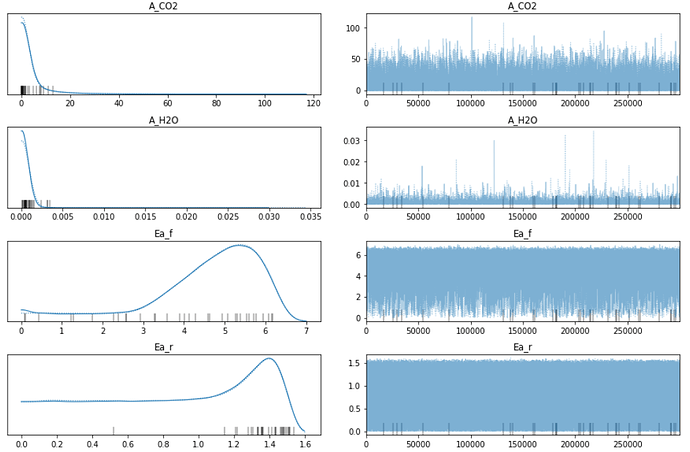
But I’m confused about the posterior traceplot:
It seems that the resulting distribution around 0 is odd. The posterior should have been a Normal Distribution, but A_CO2 and A_H2O look like Halfnormal distribution. And it seems that the distribution of Ea_r is started from 0, many sampling results distributed at 0, it looks like that the samlping less than zero is cut.
So my question is whether the function of bound is to directly remove the result below 0?
How can I explain the result of Ea_r, which is odd around zero?
And Is the sampling result of this MCMC reliable?
Thanks!