Redundant computations with multilevel models and Slice sampler

Questions v5
1

Hi everyone. I have been experimenting with developing models that have a relatively expensive black-box likelihood function (a class of “generalized” drift diffusion models). When trying to sample larger, multilevel models, I have noticed that sampling slows down incredibly as the model in question becomes more “multilevel” (e.g. more levels in a factor and/or more factors that we want to model at once). With sufficiently large models, the computation time is too long to make experimentation at all practical (e.g. easily tens or even hundreds of hours for 1000 samples). I believe I’ve found at one significant culprit and wanted to raise it here.

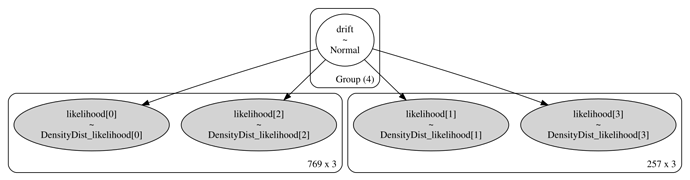
For illustration purposes, suppose we have N observations; and in the data, suppose there is one factor (data column) that has M unique levels. Finally suppose that we want to estimate a model parameter \beta_m for each of the M levels; \beta \in \mathbb{R}^M. In effect, this means that the model will have M likelihood nodes, with the mth likelihood node corresponding to the subset of data observations where the data factor is equal to the mth factor level. Each likelihood node contributes an additive term to the pymc model’s logp().

What I have noticed is that the Slice sampler seems to compute the entire model logp every time it needs a logp calculation, despite the fact that it is a univariate sampling method (only modifying one model parameter at a time, keeping all other parameters fixed). It seems to me that when the sampler is working on \beta_m, it only really needs to be evaluating the likelihood logp from the mth likelihood node—all inputs to the other likelihood nodes are remaining fixed. With a speedy pymc model, this doesn’t seem to be much of an issue. But with an expensive likelihood function, the computational cost compounds noticeably. It is worth noting that the algorithm of the slice sampler makes this particularly pronounced, because it may compute logp() many times for for every univariate proposal.

I may be wrong, but I believe that this point can be restated succinctly using the concept of the Markov blanket: although the univariate sampler working on \beta_m only needs to calculate logps via a forward-pass through the Markov blanket of \beta_m, it calculates the logp of the entire graphical model. In some cases this can be highly redundant.

  1. Does this sound correct?

    • I have had to learn a good deal just to dig through the codebase and try to track the computation graph that the sampler is calling. I am still learning and could definitely have misunderstood something :slight_smile: .

  2. Is it feasible to modify the pymc slice sampler to only perform the logp calculation using the relevant subset of the entire model graph? Feasible in terms of: statistically, is it sound; and practically, is it easy enough to do in pymc/aesara.

  3. (More to the specific use case.) Does anyone have any other suggestions for me?

    • Currently, I have hacked together a pretty sloppy caching mechanism that caches the logp outputs from each logp node, and uses the cached value if a likelihood node is given a parameter set identical to one that it has already seen. This has helped significantly, but has its limitations (cache isn’t shared across chains, introduces overhead, cache size is another tuneable parameter now).
    • In very quick-and-dirty tests with smaller models, I haven’t found any other step methods in pymc that seem more promising for sampling these models compared to the slice sampler. But I would be open to suggestions if this particular case (costly likelihood functions, many parameters, but as far as I can tell, not too “pathological” posterior geometries) seems better-suited to some other tool in the pymc toolbox. I am wondering if it may be fruitful to spend some time experimenting with using emcee as a sampler for my models in pymc, since they can at least be massively parallelized — but obviously that’s a pain because I love the pymc models as they are, and know that emcee may not be well-suited to high-dimensional models.

Sorry for the chunky post. I do try to keep it precise… Anyways, thanks as ever!

2

I think some samplers (if not slice) may be able to do this by using shared variables. They internally call make_shared_replacements or something like that. I am not quite sure which samplers do that. In those cases I think Aesara won’t recompute the nodes that depend on the shared variables that have not changed.

1 Like
3

You can try with Metropolis by passing different variables to different Metropolis samplers and checking if the computation per sample goes down as you are expecting.

If not, could you share more details of your model?

1 Like
4

Oh cool, I hadn’t known that some samplers are designed to make use of shared variables like that. Here’s a quick test based on a very simple model. However, after seeing the numbers, I think that a recent coding sprint might have messed up my ability to make use of the shared variable optimizations. I recently reworked my code to only expose one likelihood Op to the pymc model, rather than individual likelihood ops for each likelihood node (this allowed me to more easily debug the calls to each node, implement the caching feature, and explore why each sampling step was taking so long). If this makes sense, I’ll have to do some work to re-expose each likelihood node as its own Op again.

Testing models such as the following:
output
In the above model, M=4 because we’re sampling four drift rate parameters. As mentioned there’s formally four likelihood nodes, but pymc just sees one.

I can count the number of times that the aforementioned logp cache is used, for each likelihood node. Every time the cache is used, the likelihood node is getting passed a parameter set identical to a parameter set that it has seen before. For a few varying values of M (in this case, both model dimensionality and # of likelihood nodes), here are the cache counts after 100 sampling steps (slice and metropolis run separately):

M=1:
Slice: [100]
Metropolis: [100]

M=2:
Slice: [765, 841]
Metropolis: [300, 300]

M=4:
Slice: [2136, 2229, 2131, 2223]
Metropolis: [700, 700, 700, 700]

M=8:
Slice: [5216, 5204, 5138, 5153, 5153, 5133, 5145, 5118]
Metropolis: [1500, 1500, 1500, 1500, 1500, 1500, 1500, 1500]

Big differences, but Metropolis still has a lot of cache hits. I figure that this is because it’s not making use of the shared optimization; rather, the differences we see are an indication of Slice making calls to logp for each sampling step. Still an indication of the redundant computations point, but not yet able to show whether the metropolis implementation addresses it.

5

Following up on the above, I’ve now tested Metropolis and Slice on the old implementation where each likelihood node is exposed to pymc. Again we’re measuring parameter cache hits. It actually looks quite similar. Example graphical model now:

output2
output21325×347 32.9 KB

Aside from the model internals seen in the model graph, everything else should be identical. (Still 100 draws, 1 chain.)

M=1:
Slice: [200]
Metropolis: [200]

M=2:
Slice: [877, 912]
Metropolis: [400, 400]

M=4:
Slice: [2455, 2418, 2413, 2364]
Metropolis: [800, 800, 800, 800]

M=8:
Slice: [5381, 5324, 5275, 5283, 5283, 5303, 5301, 5302]
Metropolis: [1600, 1600, 1600, 1600, 1600, 1600, 1600, 1600]

If it’d help, I could code up a MWE with a simple toy model. The drift diffusion model code I have is currently a bit of a sprawling WIP so it may not be the most productive to try and work with them for this.

6

I am not sure Aesara caches results when shared variables are not updated. It was more of a guess. What you have in mind may require compiling multiple separate Aesara functions and orchestrate them together in your custom Python sampler.

7

A MWE would be cool :wink:

1 Like
8

Sorry it took a little bit, but here’s a notebook: colab notebook

The idea is just a simple recovery of 1-D gaussians; hopefully an easy task for the samplers. In summary: the notebook generates data from univariate Normal distributions, a different distribution for each of M groups. Then it tries to recover the parameters of those distributions using MCMC. It keeps track of a few statistics for each likelihood node: number of logp calls, number of unique distribution parameters seen, and number of repeat parameters seen. In order to do that, the Normal likelihood is a DensityDist wrapping an Aesara op for each node; and the op uses a cache to map parameter values to already-computed logps. It tries sampling with Slice and Metropolis on datasets generated from M=2^0,\dots,2^4 groups. I think it makes sense to keep the total number of observations fixed, so that’s what it does here.

And here’s a summary of those statistics for each run!

image
image2661×489 60.8 KB

Interesting to note that the number of logp() calls to each likelihood node seems to grow linearly, as does the number of logp() calls with repeated parameter values. Also interesting to see that the number of unique parameter vals seen by each node doesn’t really change as M changes. But as the number of groups (and hence likelihood nodes) also grows linearly, computation time grows exponentially.

9

Sorry to bump. I’m curious whether a change to Slice could help resolve this issue for that step method. Could it be possible to change the calls to logp such that Slice doesn’t even calculate the logp for nodes that are not relevant to the parameter being sampled?

Taking a deep deep dive, it looks like old pymc2 does this by keeping calculating logp on the markov blanket of the node(s) that it is sampling (link). Slice sampler just uses the logp function from self.model.compile_logp(). I don’t have a deep familiarity with aesara yet, but it seems like we perhaps we could do the same thing by compiling a different logp function?

10

You can compile a different logp function by hand, but actually Slice already doing that as @ricardoV94 said above. Basically, for Slice sampling (and any compound step, see Compound Steps in Sampling — PyMC3 3.11.5 documentation), the log_prob function each Step method using is a conditional log_prob.

11

I think what you have in mind is a bit more like what metropolis does, where it compiles a function of the delta logp, so that terms that are constant can be cancelled out: pymc/metropolis.py at 7a5074e2d4d7514784b6542cbb2f02d843549739 · pymc-devs/pymc · GitHub

I am not sure if slice sampling can work based on the delta logp.

If it could, it also matters how complicated the code would need to be.

12

PyMC can definitely compute the logp for a single variable, when you call model.logp(vars=x). You can check if Slice can work like that or of it needs the whole model logp to make correct transitions.

I am not familiar with theory/ literature on using Slice for subsets of variables.