Sampling from a NormalMixture with wide spread of parameters

[dhajnes]

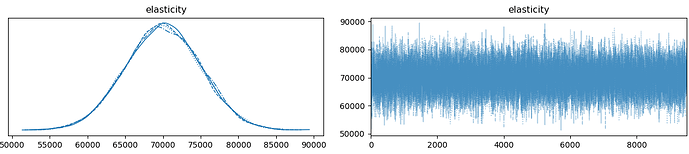
Hello,

I am trying to sample from a Gaussian Mixture (pm.NormalMixture()) that has two (as an illustratory example, in practice there’s more, e.g. 8 - 36) Normals mixed, although their means are too far away from each other.

Here: N_1(300, 100^2) and N_2(70000, 5000^2)
The mixture is mixed with weights 0.7 \cdot N_1 + 0.3 \cdot N_2, where the weights are based on a Dirichlet distribution, which is above the NormalMixture in the hierarchy.

Although when I sample the posterior of the NormalMixture, there is mainly the N_2, which should not happen. It should be more of the N_1.

The code used to generate the following graphs:

with pm.Model() as miniBN:
    mat = pm.Dirichlet('mat', a=mat_probs)
    elasticity = pm.NormalMixture('elasticity', w=mat, mu=ELAS_MUS, sigma=ELAS_SIGS)
    burn_in = 500
    trace = pm.sample(10000, tune=5000, target_accept=0.9)
    chain = trace[burn_in:]
    pm.plot_trace(chain)
    pm.plot_posterior(chain)
    plt.show()

Question:

Am I just undersampling? Should I sample more? It does not seem to help if I ramp up the sampling to say pm.sample(50000, tune=1000, target_accept=0.9). What is the proper way of handling such situations?

Graphs:

Trace:

Posterior:

[chartl]

Try using SMC instead of NUTS.

Sampling from distributions with multiple peaks with standard MCMC methods can be difficult, if not impossible, as the Markov chain often gets stuck in either of the minima. A Sequential Monte Carlo sampler (SMC) is a way to ameliorate this problem.

https://docs.pymc.io/en/v3/pymc-examples/examples/samplers/SMC2_gaussians.html

[dhajnes]

Hi @chartl,

thanks for you reply. I have tried the Sequential sampling, although it looks like there is a problem of practically zero values between the two peaks. It’s basically a zero plane between (\mu=300) and (\mu=70000). That may be a reason why it retrusn LinAlgError: singular matrix.

Do you have any proposal how to go around this problem? Perhaps adding some really small value? That would probably end up in the use of general Mixture() which I would like to avoid.

[ricardoV94]

I guess it’s just impossible to jump from one mode to the other. You might be better of using a non marginal mixture here, with a latent indicator variable and two latent normals for the modes