Context
I am attempting to fit a custom probability distribution using the VI methods. I am automating the fitting (and recording of results) so that I can apply it to ~100k separate data sets.
Data
The data points in each data set take on integer values only.
Model
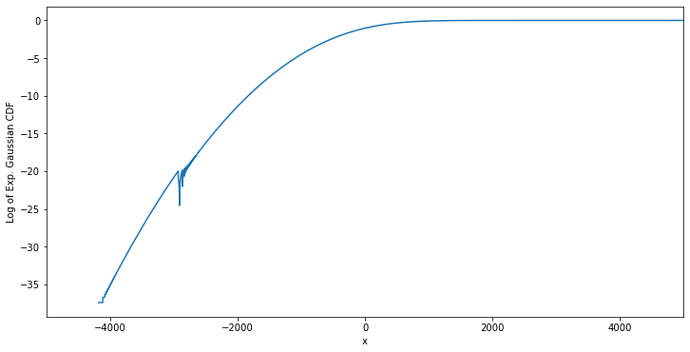
The custom PDF is proportional to the product of a CDF function (specifically that of the EMG – _emg_cdf() below) and the survival function (i.e. 1 - CDF) of the normal distribution (_norm_sf() below). Because this product cannot be analytically normalized, I am numerically computing the normalization factor at each iteration (using a large integration range) in order to scale the CDF * SF product to unity. Here’s an example of the model PDF (blue) and an example of a corresponding dataset (orange):

Code
Both the _emg_cdf and _norm_sf functions are written using base theano functions. Furthermore, the numeric normalization method is also expressed in terms of theano functions (see _min, _max, and _x). The logp of the pdf is returned and is converted to a pymc3 variable using the pm.DensityDist method. See below for the model code (Note: I’m using the T.printing.Print calls to track the parameter values for each fitting iteration):
import numpy as np
import theano.tensor as T
import pymc3 as pm
# Build model
with pm.Model() as m:
m0p=pm.Uniform('mL', lower=-200, upper=200)
s0p=pm.Uniform('sL', lower=20, upper=2000)
t0p=pm.Uniform('tI', lower=20, upper=2000)
m1p=pm.Uniform('mT', lower=4500, upper=10500)
s1p=pm.Uniform('sT', lower=30, upper=2000)
m0 = T.printing.Print('m0')(m0p)
s0 = T.printing.Print('s0')(s0p)
t0 = T.printing.Print('t0')(t0p)
m1 = T.printing.Print('m1')(m1p)
s1 = T.printing.Print('s1')(s1p)
# Custom distribution ========================================================
def _emg_cdf(x, mu, sigma, tau):
# z = (x - mu) / sigma
def _norm_cdf(z):
return 0.5 * (1 + T.erf(z / T.sqrt(2.0)))
z = (x - mu) / sigma
invK = sigma / tau
exparg = invK * (0.5 * invK - z)
logprod = exparg + T.log(_norm_cdf(z - invK))
cdf = T.abs_(_norm_cdf(z) - T.exp(logprod))
return cdf
def _norm_sf(x, mu, sigma):
arg = (x - mu) / (sigma * T.sqrt(2.0))
return 0.5 * T.erfc(arg)
def custom_logp(x):
# Unnormalized distribution value
_prob_unscaled = (
_emg_cdf(x, mu=m0, sigma=s0, tau=t0) *_norm_sf(x, mu=m1,sigma=s1)
)
# Compute norm factor by integrating over entire distribution
_n = 10 #number of stdevs for numerical normalization
_min = T.floor(T.min([m0 - _n*s0, m1 - _n*s1]))
_max = T.ceil(T.max([m0 + _n*np.sqrt(s0**2 + t0**2), m1 + _n*s1]))
_x = T.arange(_min, _max, dtype='int64')
# Generate all values, to be summed for normalization factor
_norm_array = (
_emg_cdf(_x, mu=m0, sigma=s0, tau=t0) * _norm_sf(_x, mu=m1, sigma=s1)
)
_norm_factor = T.sum(_norm_array)
# Scale distribution to true pdf
custom_prob = _prob_unscaled / _norm_factor
# Compute log-likelihood
log_pdf = T.log(custom_prob)
return log_pdf
#=============================================================================
# Convert Theano log-prob func into observed pymc3 distribution variable
custom_pdf = pm.DensityDist('custom_pdf', custom_logp, observed=rvs)
Fitting Error
I’m fitting using the ADVI class. This process seems highly unstable and inconsistent—if I tweak the prior parameters a bit or change the random_seed value, the fitting process will sometimes complete without error, however much of the time the fit is halted on an ValueError due to some of the parameters taking on a nan value. Running following fitting code (after the above model code):
with m:
vi = pm.ADVI(random_seed=42)
approx = vi.fit(10000, progressbar=False)
Errors with the following:
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
~\Miniconda3\envs\dowell\lib\site-packages\theano\compile\function_module.py in __call__(self, *args, **kwargs)
902 outputs =\
--> 903 self.fn() if output_subset is None else\
904 self.fn(output_subset=output_subset)
~\Miniconda3\envs\dowell\lib\site-packages\theano\gof\op.py in rval(p, i, o, n)
891 def rval(p=p, i=node_input_storage, o=node_output_storage, n=node):
--> 892 r = p(n, [x[0] for x in i], o)
893 for o in node.outputs:
~\Miniconda3\envs\dowell\lib\site-packages\theano\tensor\basic.py in perform(self, node, inp, out_)
5542 step = step.item()
-> 5543 out[0] = np.arange(start, stop, step, dtype=self.dtype)
5544
ValueError: arange: cannot compute length
...[Ive omitted some of the error]...
ValueError: arange: cannot compute length
Apply node that caused the error: ARange{dtype='int64'}(Elemwise{Floor}[(0, 0)].0, Elemwise{Ceil}[(0, 0)].0, TensorConstant{1})
Toposort index: 99
Inputs types: [TensorType(float64, scalar), TensorType(float64, scalar), TensorType(int8, scalar)]
Inputs shapes: [(), (), ()]
Inputs strides: [(), (), ()]
Inputs values: [array(nan), array(nan), array(1, dtype=int8)]
Outputs clients: [[Elemwise{sub,no_inplace}(ARange{dtype='int64'}.0, InplaceDimShuffle{x}.0), Elemwise{sub,no_inplace}(ARange{dtype='int64'}.0, InplaceDimShuffle{x}.0)]]
Printing the parameter values for the last few iterations of the fit (using T.printing.Print) I see the nan values that produce the error:
...
m0 __str__ = -106.98177137073989
s0 __str__ = 564.1090064087261
t0 __str__ = 283.4875869828139
m1 __str__ = 5563.1240925511665
s1 __str__ = 485.17358772825014
m0 __str__ = 26.688642526520788
s0 __str__ = 153.88894549775893
t0 __str__ = 419.6344762064323
m1 __str__ = 6306.569380878885
s1 __str__ = 1364.1750774031318
m0 __str__ = nan
s0 __str__ = nan
t0 __str__ = nan
m1 __str__ = 5909.70120440209
s1 __str__ = 612.2725062193786
[ERRORS HERE]
This doesn’t appear to be a problem with my model. If I evaluate the model using the parameter values just prior to the nan iteration, there doesn’t appear to be an issues with the PDF. Furthermore, if I adjust the parameters for the prior distributions, sometimes the fitting procedure completes without error and produces a sensible result. I am wondering if there is some issue with the theano backend that is causing this. This wouldn’t be a big issue if I were simply running the fit on a single dataset, but I am attempting to apply this fitting procedure to 100k+ datasets and ~40% of them are failing with this same issue, making it difficult to automate the fitting. Any help would be much appreciated. Thanks!
One note: I can prodvide code to simulate the above example data, if needed.
Versions
import sys, scipy, numpy, pymc3
print(scipy.__version__, numpy.__version__, pymc3.__version__, sys.version_info)
1.6.0 1.18.1 3.8 sys.version_info(major=3, minor=7, micro=6, releaselevel='final', serial=0)