Hi Community,
I am trying to implement a white paper:
1-s2.0-S0377221718309159-main copy.pdf (2.9 MB)
Cox PHM looks like this:
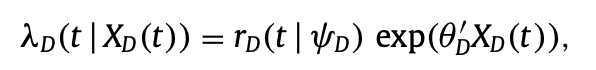
Where Lamda_D is the hazard rate for default.
r_D is the baseline hazard rate for default
Theta_D and X_D are regression parameters and covariates
In this paper they have generated the likelihood function like this :
t_d,t_p are your realization of Random Variable T_d and T_p respectively.
I am trying to convert this problem into PYMC world and haven’t been able to implement it correctly yet.
I have an input dataset where each row is a mortgage, set of covariates and time_to_default/prepayment (depends on the cause of failure). I have tried the following:
def standardize(x, mu, sigma):
return (x - mu) / sigma
def standardNormCdf(x):
return 0.5 + 0.5 * pm.math.erf(x / pm.math.sqrt(2))
def getContributionFromInterval(interval, mu, sigma):
logT = log(interval)
a = standardize(logT, mu, sigma)
return log(1 - standardNormCdf(a))
def computeFailureRate(sigma, mu, t, theta, data):
logT = log(t)
a1 = standardize(log(t), mu, sigma)
a2 = 0.5 * log(2 * pi * pow(sigma, 2))
B = 0.5 * pow(a1, 2)
C = log(1 - standardNormCdf(a1))
D = (theta * data).sum(axis=-1).reshape((-1, 1))
failureRate = ((-1) * logT) - a2 - B - C + D
return failureRate
def getSurvival(time_to_event, mu, sigma, theta, features):
contributionFromFinalInterval = (-1) * getContributionFromInterval(time_to_event, mu, sigma)
theta_features_vector = (theta * features).sum(axis=-1)
theta_features_vector = theta_features_vector.reshape((-1, 1))
survival = (contributionFromFinalInterval * theta_features_vector)
survival = survival.sum(axis=1).reshape((-1, 1))
return survival
theta_D = pm.Normal('theta_D', mu=0, sigma=100, shape=(1, features_shape[1]))
theta_P = pm.Normal('theta_P', mu=0, sigma=100, shape=(1, features_shape[1]))
mu_D = pm.Normal('mu_D', mu=0, sigma=10)
mu_P = pm.Normal('mu_P', mu=0, sigma=10)
sigma_D = pm.Exponential('sigma_D', .01)
sigma_P = pm.Exponential('sigma_P', .01)
def logp(time_to_event, mu_P, mu_D, sigma_P,
sigma_D, theta_D, theta_P, event,
features):
failureRate = where(
pt.eq(event, 0),
computeFailureRate(sigma_D, mu_D, time_to_event, theta_D, features),
where(pt.eq(event, 1),
computeFailureRate(sigma_P, mu_P, time_to_event, theta_P, features),
1)
)
defaultSurvival = getSurvival(time_to_event, mu_D, sigma_D,
theta_D, features)
prepaymentSurival = getSurvival(time_to_event, mu_P,
sigma_P, theta_P, features)
return (failureRate - defaultSurvival - prepaymentSurival).flatten().sum()
l = logp(time_to_event, mu_P, mu_D,
sigma_P, sigma_D, theta_D, theta_P,
events, features_num)
likelihood = pm.CustomDist('LL', mu_P, mu_D,
sigma_P, sigma_D, theta_D, theta_P,
events, features_num,
logp=logp,
observed=time_to_event)
# trace = pm.sampling_jax.sample_numpyro_nuts(draws=1000,tune=1000, chains=4,chain_method='parallel')
trace = pm.sample(draws=1000, tune=1000, chains=4)
return trace
Something that I am failing to understand is what goes into the observed keyword? I feel I am messing things up there.
I would be really grateful if someone could shed some light on how I could achieve this in PYMC
