Evaluating conditional covariance function of a GP

Questions v5
1

Hey there! I’ve created a simple GP model using a combination of two Matérn kernels.
I would like to compute the correlation function (matrix) for my data points. If I understood the theory correctly, I would just need the conditional covariance function from which I can simply compute the correlation function.

Question: How can I extract the conditional covariance function for some given data points?

It seems that running cov_func(X).eval() yields the prior covariance function. How would I get the conditional covariance function?

2

CC @bwengals

3

Quick update from my side - I think I found a solution, but I’d be glad if someone could confirm.

Basically, I tried to compute the conditional covariance matrix by hand (using equation 2.24 of Rasmussen’s “GPs for ML”). Here’s an example using a simple squared exponential kernel.

length_scale_mean = np.mean(trace.posterior["length_scale"].values)
eta_mean = np.mean(trace.posterior["eta"].values)
sigma_mean = np.mean(trace.posterior["sigma"].values)

# Recreate the covariance function with mean parameter values
cov_func_mean = eta_mean**2 * pm.gp.cov.ExpQuad(1, ls=length_scale_mean)

K_obs_obs = cov_func_mean(X_obs).eval()

# Add noise variance to the diagonal (assuming sigma is a scalar here)
sigma_squared = sigma_mean**2
K_obs_obs_with_noise = K_obs_obs + np.eye(len(X_obs)) * sigma_squared

# Compute the inverse
K_obs_obs_inv = np.linalg.inv(K_obs_obs_with_noise)

# Compute the posterior covariance matrix
Cov_post = K_obs_obs - np.dot(np.dot(K_obs_obs, K_obs_obs_inv), K_obs_obs)

At least for my example I get sensible results. Would someone be able to confirm that this is indeed correct? Are there potential pitfalls with this approach?

4

*Little correction in the formula - the final line for computing the posterior covariance matrix should actually be:

Cov_post = K_obs_obs_with_noise - np.dot(np.dot(K_obs_obs, K_obs_obs_inv), K_obs_obs)
5

This should work for you. It may be a little more numerically stable to use solves instead of computing the inverse directly. You could also call _build_conditional or adapt the code here

6

Thanks @bwengals ! I tried your suggestion using _build_conditional but I’m a bit stuck on this. (disclaimer: I’m relatively new to pymc, sorry if my question is trivial)

After sampling from my mode I run the following code:

jitter = 1e-6
givens = gp_hm._get_given_vals(None)
mu, cov = gp_hm._build_conditional(X, *givens, jitter)

From checking the source code + docs, I believe that providing None to _get_given_vals is fine because the gp has the required values cached (please correct me if I’m wrong).

The cov object returns Sub.0 so I thought I have to use eval. However, it seems that cov.eval(X) expects a dictionary instead of the data array X?

AttributeError: 'numpy.ndarray' object has no attribute 'items'

Evaluating the covariance matrix without input cov.eval() works but seems to produce a matrix full of zeros.

Would you mind pointing me in the right direction?

7

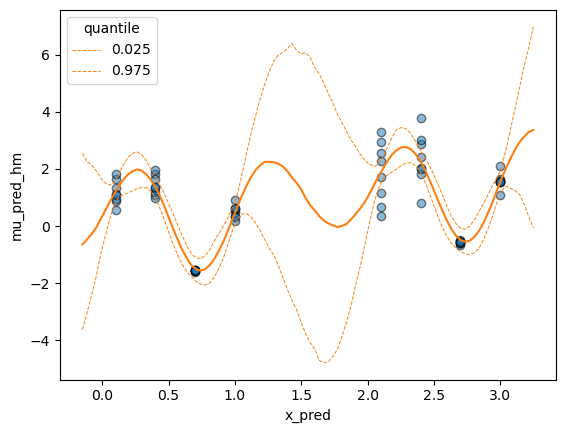
It’s probably rather simple, but I don’t understand why I cannot evaluate the conditional covariance function. I’ve adapted this example of a homoskedastic GP as a minimal working example.

1. Creating the data

import numpy as np
import pymc as pm


def signal(x):
    return x / 2 + 2 * np.sin(2 * np.pi * x)


def noise(y):
    return np.exp(y) / 10


SEED = 2020
rng = np.random.default_rng(SEED)

n_data_points = 4
n_samples_per_point = 8
X = np.linspace(0.1, 1, n_data_points)[:, None]
X = np.vstack([X, X + 2])
X_ = X.flatten()
y = signal(X_)
σ_fun = noise(y)

y_err = rng.lognormal(np.log(σ_fun), 0.1)
y_obs = rng.normal(y, y_err, size=(n_samples_per_point, len(y)))
y_obs_ = y_obs.T.flatten()
X_obs = np.tile(X.T, (n_samples_per_point, 1)).T.reshape(-1, 1)
X_obs_ = X_obs.flatten()
idx = np.tile(
    np.array([i for i, _ in enumerate(X_)]), (n_samples_per_point, 1)
).T.flatten()

Xnew = np.linspace(-0.15, 3.25, 100)[:, None]
Xnew_ = Xnew.flatten()
ynew = signal(Xnew)

2. Fit the model

coords = {"x": X_, "sample": np.arange(X_obs_.size)}

with pm.Model(coords=coords) as model_hm:
    _idx = pm.ConstantData("idx", idx, dims="sample")
    _X = pm.ConstantData("X", X, dims=("x", "feature"))

    η = pm.Exponential("η", lam=1)
    ell_params = pm.find_constrained_prior(
        pm.InverseGamma, lower=0.1, upper=3.0, init_guess={"mu": 1.5, "sigma": 0.5}
    )
    ℓ = pm.InverseGamma("ℓ", **ell_params)
    cov = η**2 * pm.gp.cov.ExpQuad(input_dim=1, ls=ℓ) + pm.gp.cov.WhiteNoise(1e-6)
    σ = pm.Exponential("σ", lam=1)

    gp_hm = pm.gp.Latent(cov_func=cov)
    f = gp_hm.prior("f", X=_X)
    ml_hm = pm.Normal("ml_hm", mu=f[_idx], sigma=σ, observed=y_obs_, dims="sample")

    trace_hm = pm.sample(
        500,
        tune=1000,
        chains=1,
        return_inferencedata=True,
        random_seed=SEED,
        nuts_sampler="numpyro",
    )

3. Make predictions

with model_hm:
    model_hm.add_coords({"x_pred": Xnew_})
    mu_pred_hm = gp_hm.conditional("mu_pred_hm", Xnew=Xnew, dims="x_pred")
    samples_hm = pm.sample_posterior_predictive(
        trace_hm, var_names=["mu_pred_hm"], random_seed=42
    )

output

4. Sampling the posterior covariance function

Until here, everything looks fine to me. Now, I’d like to sample the posterior covariance function for my observed data.

with model_hm:
    jitter = 1e-6
    givens = gp_hm._get_given_vals(None)
    mu2, cov2 = gp_hm._build_conditional(_X, *givens, jitter)

And this is where I’m stuck… How do I obtain the 8x8 covariance matrix for the observed data locations?

8

Hey @nrieger, sorry for the slow response. You can set the new covariance you make as a deterministic, then do posterior predictive sampling, like this:

with model_hm:
    model_hm.add_coords({"x_pred": Xnew_})
    mu_pred_hm = gp_hm.conditional("mu_pred_hm", Xnew=Xnew, dims="x_pred")
    
    jitter = 1e-6
    givens = gp_hm._get_given_vals(None)
    mu2, cov2 = gp_hm._build_conditional(_X, *givens, jitter)
    cov2 = pm.Deterministic("cov2", cov2)
    
    trace_hm.extend(pm.sample_posterior_predictive(
        trace_hm, var_names=["mu_pred_hm", "cov2"], random_seed=42
    ))

    
import arviz as az
cov2 = az.extract(trace_hm, group="posterior_predictive", var_names="cov2")

cov2.shape
1 Like
9

No stress @bwengals ! I have the utmost respect for the work and time you invest here on Discourse. If you’re taking the time to look through and answer my questions, then you can take as much time as you need. :slight_smile:

Using pm.Deterministic makes it work without a problem (thanks for that!). However, I still have my doubts about the results. From the picture above showing the posterior predictive distributions, I would expect that

  • the diagonal of the covariance matrix is not equal to zero
  • the cross-covariance terms between the individual x_pred locations are also not equal to zero

However, when I read out the conditioned covariance matrix and look at the sample mean, I get a diagonal matrix with 1e-6 on the diagonal, which is obviously just the jitter term. Have I fundamentally misunderstood something here? Somehow it’s still not clear to me how to read out the conditioned covariance matrix…

UPDATE: Sampling the covariance matrix using new data seems to work! However, with the data locations used for fitting the model, is does not seem to work i.e. only produces the jitter matrix.

This works

mu2, cov2 = gp_hm._build_conditional(Xnew, *givens, jitter)

This doesn’t

mu2, cov2 = gp_hm._build_conditional(_X, *givens, jitter)

The difference (apart from other x locations, obviously) is that Xnew is a pure 2D numpy array, while _X is a TensorConstant. I don’t know enough about the internals of pymc to understand why that makes a difference, but this behavior seems slightly non-intuitive for me as pymc novice. It this behavior expected?

10

Again, super late. You’ve probably moved on but, I checked and I had a bug in my answer. Here’s the corrected version:

with model_hm:

    jitter = 1e-6
    givens = gp_hm._get_given_vals(None)
    mu2, cov2 = gp_hm._build_conditional(Xnew, *givens, jitter)
    
    mu2 = pm.Deterministic("mu2", mu2)
    cov2 = pm.Deterministic("cov2", cov2)
    
    trace_hm.extend(pm.sample_posterior_predictive(
        trace_hm, var_names=["mu2", "cov2"], random_seed=42
    ))

    
import arviz as az
cov2 = az.extract(trace_hm, group="posterior_predictive", var_names="cov2")

import matplotlib.pyplot as plt

plt.imshow(cov2[:, :, 0]); plt.colorbar();

The line of shame is

    mu2, cov2 = gp_hm._build_conditional(_X, *givens, jitter)

Should feed in Xnew there, not _X! That explains why it was the wrong size and equal to jitter * np.eye(8).

1 Like