Hello,
I’m getting a dimensionality error trying to graph my model but can’t find where the error is.
---------------------------------------------------------------------------
ShapeError Traceback (most recent call last)
/tmp/ipykernel_11866/2705921953.py in <module>
86 predictions,
87 observed=eaches,
---> 88 dims='obs_id'
89 )
90
/opt/conda/lib/python3.7/site-packages/pymc/distributions/distribution.py in __new__(cls, name, *args, **kwargs)
592 raise ValueError("Transformations for discrete distributions")
593
--> 594 return super().__new__(cls, name, *args, **kwargs)
595
596
/opt/conda/lib/python3.7/site-packages/pymc/distributions/distribution.py in __new__(cls, name, rng, dims, initval, observed, total_size, transform, *args, **kwargs)
276 dims=dims,
277 transform=transform,
--> 278 initval=initval,
279 )
280
/opt/conda/lib/python3.7/site-packages/pymc/model.py in register_rv(self, rv_var, name, data, total_size, dims, transform, initval)
1311 # `rv_var` is potentially changed by `make_obs_var`,
1312 # for example into a new graph for imputation of missing data.
-> 1313 rv_var = self.make_obs_var(rv_var, data, dims, transform)
1314
1315 return rv_var
/opt/conda/lib/python3.7/site-packages/pymc/model.py in make_obs_var(self, rv_var, data, dims, transform)
1338 if data.ndim != rv_var.ndim:
1339 raise ShapeError(
-> 1340 "Dimensionality of data and RV don't match.", actual=data.ndim, expected=rv_var.ndim
1341 )
1342
ShapeError: Dimensionality of data and RV don't match. (actual 1 != expected 2)
When I try to insert a delta.shape.eval() or m.shape.eval() I then get the following error.
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
/tmp/ipykernel_11866/4216889251.py in <module>
52 mu_delta = pm.Laplace('mu_delta', 0,1, shape=(n_groups, n_changepoints), dims='location')
53 delta = pm.Deterministic('delta', sigma_delta*mu_delta)
---> 54 delta.shape_eval()
55 growth = ((k[group] + at.dot(a_, delta[group])))
56 offset = ((m[group] + at.dot(a_, -s_ * delta[group])))
AttributeError: 'TensorVariable' object has no attribute 'shape_eval'
For reference, here is my model code.
n_changepoints = 8
t = np.arange(len(df_train)) / len(df_train)
s = np.linspace(0, np.max(t), n_changepoints+2)[1:-1]
a = (t[:, None] > s)*1
n_components = 10
group = df_train['location'].cat.codes.values
group_mapping = dict(enumerate(df_train['location'].cat.categories))
n_groups = df_train['location'].nunique()
location_idxs, locations = pd.factorize(df_train['location'])
coords_={
"location":df_train['location'].unique(),
"obs_id":np.arange(len(location_idxs))
}
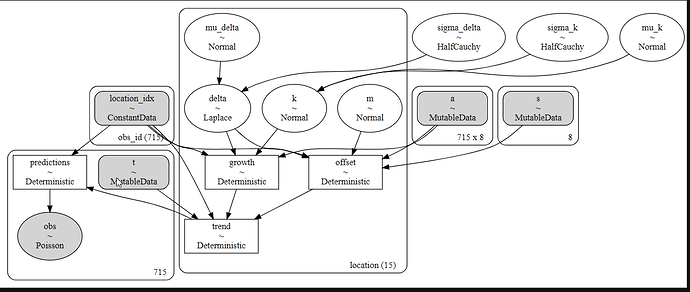
with pm.Model(coords=coords_) as partial_pooled_model:
location_idx = pm.ConstantData('location_idx', location_idxs, dims = 'obs_id')
t_ = pm.MutableData('t', t)
a_ = pm.MutableData('a', a)
s_ = pm.MutableData('s', s)
eaches = pm.MutableData('eaches', df_train['eaches'])
mu_k = pm.Normal('mu_k', 0,100, shape = n_groups, dims = 'location')
sigma_k = pm.HalfNormal('sigma_k', 5)
k = pm.Deterministic('k', mu_k*sigma_k)
m = pm.Normal('m', 0, 5, shape = n_groups)
sigma_delta = pm.HalfCauchy('sigma_delta', .05)
mu_delta = pm.Laplace('mu_delta', 0,1, shape=(n_groups, n_changepoints), dims='location')
delta = pm.Deterministic('delta', sigma_delta*mu_delta)
growth = ((k[group] + at.dot(a_, delta[group])))
offset = ((m[group] + at.dot(a_, -s_ * delta[group])))
trend = pm.Deterministic('trend', growth * t_ + offset)
predictions = pm.Deterministic('predictions', np.exp(trend[location_idx]))
pm.Poisson('obs',
predictions,
observed=eaches,
dims='obs_id'
)
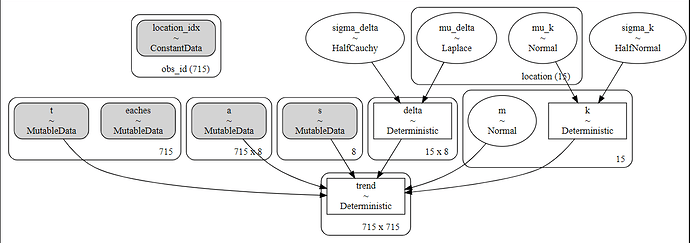
pm.model_to_graphviz( partial_pooled_model)
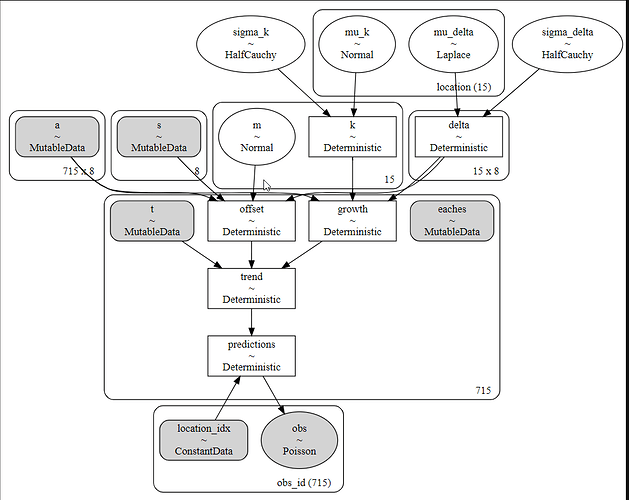
Code adapted from @MBrouns repo timeseers/timeseries_model.py at master · MBrouns/timeseers (github.com)
UPDATE:
I took out the PM.Poisson... code at the end and got it to graph this:
I’m not sure how trend is ending up with 715x715 shape or how to fix it.