Hi all,
CONTEXT
I have a data set comprising sensor data collected every second. After doing some basic analysis I discovered that the standard deviation of the weekday (WD) data and the weekend (WE) data is significantly different. This is not the case for the mean, which in both subsets (i.e. WD and WE) is basically the same.
WHAT I’VE DONE
To get estimates of the posterior of the mean and sigma I have implemented two simple Gaussian models one for each of WD and WE. The results are satisfactory.
PROBLEM
I’m trying to analyze both WD and WE as a single data set feeding it to a Mixture model expecting to get the same results I am getting if I manually split the data. However the results obtained can’t find that there are sort of two levels (or layers in the data). The first being the parameters that describe the data as a whole and the second level the split of the data in weekdays and weekends. The mixture model finds the parameters of the first layer. That is, that in the WD+WE data set there exist two big clusters, each with its own mean but fails to find the parameters of the WD and WE individually.
How can I go about this?
I hope this all makes sense, otherwise please let me know I’ll try to be clearer.
ATTEMPT
Takes as input WD and WE concatenated. I have tried with a shape=4 but the results are basically the same as shape=2
y = pd.read_pickle('means_df_01')
new_df=pd.DataFrame()
new_df['WD']=pd.to_numeric(y.iloc[:-1,0])
new_df['WE']=pd.to_numeric(y.iloc[:-1,1])
data = new_df['WD'].values.tolist()
data = data + new_df['WE'].values.tolist()
with pm.Model() as model:
w = pm.Dirichlet('p', a=np.ones(2))
mu = pm.Normal('mu', 0, 20, shape=2,testval=[-10, 10])
sigma = pm.HalfNormal('sigma', sd=2, shape=2)
pm.NormalMixture('like',w=w,mu=mu,sd=sigma,observed=data)
trace = pm.sample(tune=2000, target_accept=0.9, random_seed=20191121)
PLOTS
As you can see in the next plot, taking WD+WE as a single data set, it is possible to see two main clusters: mean ~ 2 and 7 respectively.
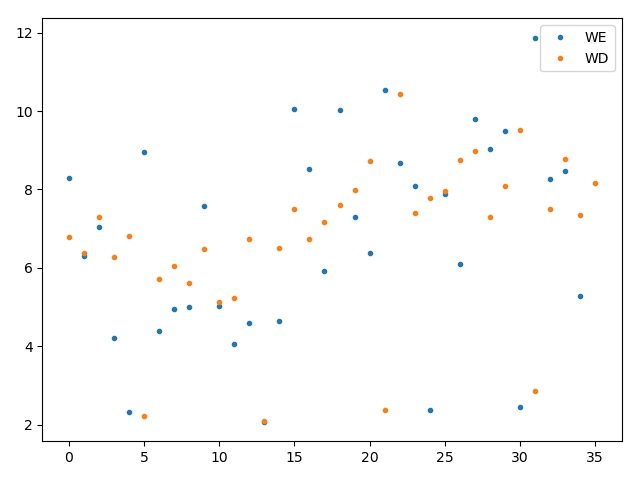
If I manually split the data and use a Gaussian model I get accurate estimates for the posterior of the mean and sigma. The interesting part is the how different are both sigmas:
https://github.com/jnew123/tmp-plots/blob/master/gaussian_model.png
The next plot shows the results of a single dataset and a mixture model. As you can see it discovers only the upper level parameters. I tried estimating 4 parameters instead of two but the results were almost identical.
[https://github.com/jnew123/tmp-plots/blob/master/mixture_model_1.png)
I’m only allowed to upload one image.
Many Thanks. 