How to get postierior predictive mean in az.plot_ppc

Questions version agnostic
,
1

Hi every one:
I have created a Dirichlet mixture binomial model using PyMC5. The posterior predictive mean in az.plot_ppc seems to fit the observations well. However, the plot showed significant differences when I computed the posterior predictive mean using code similar to idata.posterior_predictive['var_name'].mean(dim=["chain","draw"]) . As a result, the posterior predictive mean obtained was different. How can I obtain the same posterior predictive mean as the one generated by az.plot_ppc ?

image
image

image
image

below was my code

ad_ar = np.array([ 80., 185., 189.,  71.,  66., 121., 131.,  65., 135., 176.,  49.,
       111.,  91., 100., 178.,  72., 135.,  83., 130.,  75., 180., 160.,
        65., 193.,  50.,  82., 118., 123., 161., 183., 211., 119., 206.,
        57., 173.,  58., 134.,  89., 138., 147., 162., 186., 125.,  81.,
       163., 116., 112.,  77., 105., 207., 161., 158.,  53.,  61., 157.,
        79., 121., 152., 113., 111., 179.,  75.,  83.,  78., 161., 134.,
       205.,  86.,  67.,  90., 133., 146., 127., 170., 152.,  65., 126.,
        73.,  56., 149., 187., 173.,  57., 146.,  78., 186., 173., 136.,
       220., 159., 169., 139., 162.,  67.,  54., 113., 128., 156.,  88.,
       198., 134., 194.,  63., 145., 200., 152., 214., 144., 171., 177.,
        64.,  87.,  58., 154.,  84.,  80., 163., 192.,  63., 167.,  83.,
        85.,  51.,  73.,  78., 119., 139., 192.,  96.,  69., 153., 139.,
       165., 160., 120., 129., 164., 239., 114.,  90., 140.,  87., 131.,
        60., 130.,  70.,  89., 105.,  70.,  86.,  93., 132., 176.,  70.,
       148.,  66.,  55., 138.,  60., 184., 127., 144.,  71., 158., 183.,
       136.,  72., 102., 185., 146., 128., 134., 161.,  83., 135.,  69.,
       104., 141., 193.,  85., 197.])
dp_ar = np.array([190., 185., 189., 151., 124., 231., 131., 118., 136., 176., 113.,
       204., 161., 213., 179., 146., 135., 160., 130., 146., 180., 160.,
       135., 193., 133., 160., 118., 254., 161., 183., 211., 119., 206.,
       117., 173., 113., 134., 157., 138., 147., 162., 186., 125., 182.,
       163., 116., 112., 155., 105., 207., 161., 158., 114., 120., 158.,
       162., 121., 153., 113., 111., 179., 142., 162., 157., 161., 134.,
       206., 164., 145., 197., 133., 146., 127., 172., 152., 153., 126.,
162., 127., 149., 188., 173., 125., 146., 152., 186., 173., 136.,
       220., 159., 169., 140., 162., 140., 119., 113., 128., 156., 173.,
       198., 134., 194., 138., 145., 200., 153., 215., 144., 171., 178.,
       116., 174., 130., 154., 175., 157., 163., 192., 131., 167., 161.,
       145., 117., 156., 153., 119., 139., 192., 182., 156., 153., 139.,
       165., 160., 120., 129., 164., 239., 115., 178., 140., 161., 132.,
       132., 130., 145., 166., 105., 149., 167., 187., 132., 177., 149.,
       148., 151., 153., 139., 138., 184., 127., 145., 171., 158., 184.,
       136., 139., 183., 185., 146., 129., 134., 161., 199., 135., 132.,
       104., 141., 193., 156., 197.])

K = 20
N = ad_ar.shape[0]
b = get_beta_param(vaf_ar.mean())
with pm.Model(coords={"component": np.arange(K), "obs_id": np.arange(N)}) as model:
    alpha = pm.Gamma("alpha", 1.0, 1.0)
    cond = alpha>1
    alpha_constrained = pm.Potential('alpha_constrained',pm.math.log(pm.math.switch(cond, 1, 0)))  
    beta = pm.Beta("beta", 1, alpha, dims="component")
    w = pm.Deterministic("w", stick_breaking(beta), dims="component")
    p = pm.Beta("p",1,1,dims="component")

    obs = pm.Mixture(
        "ad", w, pm.Binomial.dist(n=dp_ar.reshape(-1,1),p=p), observed=ad_ar, dims="obs_id"
    )

########## plot
ppc = trace.posterior_predictive["ad"]

ppc_mean = ppc.mean(dim=["chain","draw"])

az.plot_ppc(trace,var_names="ad",num_pp_samples=100)

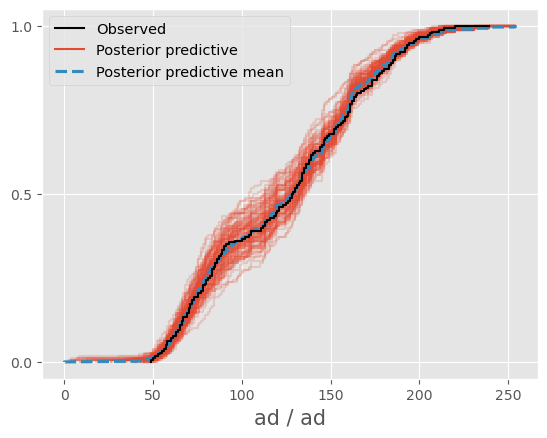
az.plot_ppc(trace,var_names="ad",num_pp_samples=100,kind="cumulative")
az.plot_ppc(trace,var_names="ad",num_pp_samples=100,kind="cumulative")

ax = sns.kdeplot(ppc_mean,color="blue")
sns.kdeplot(trace.observed_data["ad"].values,color="red")

ax = sns.ecdfplot(ppc_mean,color="blue")
sns.ecdfplot(trace.observed_data["ad"].values,color="red",ax=ax)
2

In the bayesian paradigm, the observations are fixed, but taken to be a realization/sample from a random variable. When doing posterior predictive sampling on the same data the model was fitted on, each draw simulates that observation/sample, and as you have multiple observations and assume all coke from the same distribution, we can generate a histogram/kde/cdf fir every single draw. These are the red lines in your plot, the black line from the observations is a similar thing, but for your observations, so it can only be one line. The “posterior predictive mean” is the histogram of all posterior predictive samples (all observations and all draws). Kdes, histogrms… all have some randomness still in them, so it can be useful to have also rhis somewhat less noisy visualization.

When you take the mean, you are not comparing “equivalent” realizations. It would be saying that your observation process is not taking draws from the random variable in your model but taking s samples of n observations each and then take the mean over the samples to get the n observations. It is not exactly tye “distribution of the mean” instead of the “mean distribution” (what the dashed line in plot ppc attempts to be) but the “distribution of pointwise means”, something like that

1 Like