Implementing a simple toy scenario with probabilistic reasoning in pymc

Questions version agnostic
1

Hi, I have a question regarding a relatively simply probabilistic programming example that involves discrete variables. The example is taken from Chapter 1 of the book “Practical Probabilistic Programming” (see Table 1.1 here: Chapter 1. Probabilistic programming in a nutshell - Practical Probabilistic Programming (manning.com)).

I implemented this scenario in WebPPL ( WebPPL - probabilistic programming for the web) (see this gist: webppl example (github.com)) and now I am wondering whether it is possible to implement the same example in pymc3.

Here is the scenario:

  • Assume the weather can have two states sunny and not sunny with the following (prior) probabilities:
    • Sunny 0.2
    • Not sunny 0.8
  • Based on the weather, we will be greeted with different greetings according to the following probabilistic logic:
    • If today’s weather is sunny
      • “Hello, world!” 0.6
      • "Howdy, universe!” 0.4
    • If today’s weather isn’t sunny
      • “Hello, world!” 0.2
      • "Oh no, not again” 0.8

No, we want to do two things:

  • Simulate today’s greeting based on the (prior) probability of seeing sunny weather
  • Infer today’s weather based on an observed greeting

I implemented the first task using pm.sample_prior_predictive() with this code:

import altair as alt
import numpy as np
import pandas as pd
import pymc as pm
from aesara.ifelse import ifelse

g0 = "Hello, World!"
g1 = "Howdy, universe!"
g2 = "Oh no, not again!"
greetings = np.array([g0, g1, g2])
weather_states = np.array(["cloudy", "sunny"])

def greeting(model, sunny):
    if model is None:
        model = pm.Model()
    with model:
        p_choice = ifelse(sunny, 0.6, 0.2)
        altAnswer = pm.Deterministic('altAnswer', ifelse(sunny, 1, 2))
        greeting = pm.Deterministic('GreetingToday', ifelse(pm.Bernoulli("GreetingChoice", p_choice), 0, altAnswer))
    return model

def predictGreetingToday():
    p_sunny = 0.2
    with pm.Model() as model:
        sunny = pm.Bernoulli("sunny", p_sunny)
        greeting(model, sunny)
    return model

trace = pm.sample_prior_predictive(1000, model=predictGreetingToday())

# Plot the results
sunny_df = pd.DataFrame(
    {"weather": weather_states[np.array(trace.prior["sunny"]).reshape(-1)]}
)
weather_chart = alt.Chart(
    sunny_df.value_counts(normalize=True).reset_index().rename(columns={0: "count"})
).mark_bar().encode(x="weather:N", y="count:Q")

greeting_df = pd.DataFrame(
    {"greeting": greetings[np.array(trace.prior["GreetingToday"]).reshape(-1)]}
)
greeting_chart = alt.Chart(
    greeting_df.value_counts(normalize=True).reset_index().rename(columns={0: "count"})
).mark_bar().encode(x="greeting:N", y="count:Q")
weather_chart | greeting_chart

giving something like this:
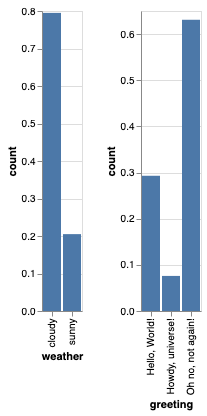
visualization (8)

However, I am struggling to implement the 2nd task, i.e., to do some inference. The main problem is that it is not possible to do inference on the deterministic variable greeting, which is what we observe. I think I could make it work implementing the backward logic manually, i.e., do something like this:

if greeting == g2:
    altAnswer_obs = g2
    sunny = False
elif greeting == g1:
    altAnswer_obs = g1
    sunny = True
else:
    ...
    # not sure what do do here

However, even if that would work, this is not really the point, because the point of Probabilistic Programming, generally speaking, is to do this kind of probabilistic reasoning on its own, right?

I understand that this is not really the typical use case of pymc3 but I am trying to understand the difference between different PPLs, like e.g. webPPL and pymc3, so is it possible at all do implement this scenario in pymc3?
WebPPL can solve this task either with exact enumeration (which is feasible for these simple cases with discrete variables) or rejection sampling.
If not, are there other PPLs implemented in python that can do this?

2

To do conditional inference, you can look at subsets of your trace given the conditions you are interested in.

For example, if you want to know p(sunny | greeting = “Howdy, universe!”), first get all samples that correspond to the greeting “Howdy, universe”, then look at the distribution of values of “sunny” for those samples. Given your code, it should be something like:

greeting_mask = greeting_df.values == 'Howdy, universe'
sunny_given_greeting = sunny_df.loc[greeting_mask]

As a sanity check, these should all be “sunny”.

3

Thanks for the quick reply. Yes, that would essentially mean that we implement rejection sampling manually, right?

4

You can take a look at this thread: Bayes Nets, Belief Networks, and PyMC
@drbenvincent might have done some follow-up work on this as well.

1 Like
5

Also, in your case it is perfectly possible to have everything end to end in PyMC, the trick is to pad the “missing” greeting:

weather_prob = np.asarray([.2, .8])  # Sunny, Not sunny
greeting_prob = np.asarray([[.6, .4, 0.],   # <= notice how the missing greeting has 0 probability
                            [.2, 0., .8]])

with pm.Model() as m:
    observed = pm.Data('observed', 0, mutable=True)
    weather = pm.Categorical('weather', weather_prob)
    greeting = pm.Categorical('greeting', 
                              aesara.shared(greeting_prob)[weather], 
                              observed=observed)
    # Simulate today’s greeting based on the (prior) probability of seeing sunny weather
    prior_sample = pm.sample_prior_predictive(1000)

# Infer today’s weather based on an observed greeting
traces = []
for obs in range(3):
    with m:
        observed.set_value(obs)
        traces.append(pm.sample(initvals={'weather': max(0, obs-1)}))

You can see that the result is the same as indexing to the prior_predictive @jessegrabowski explained:

_, axes = plt.subplots(1, 2, figsize=(5, 5), sharey=True)
for i, trace in enumerate(traces):
    x, y = np.unique(trace.posterior['weather'], return_counts=True)
    axes[0].bar(x + (i-1) / 5, y/y.sum(), width=.2);
    x_, y_ = np.unique(
        prior_sample.prior['weather'].values[prior_sample.prior_predictive['greeting'].values == i],
        return_counts=True)
    axes[1].bar(x_ + (i-1) / 5, y_/y_.sum(), width=.2);
axes[0].legend([f'observed = {i}' for i in range(3)])

image

6

Thanks, I just had the same thought, looking at the thread you had linked to. Thanks for your reply!

But more generally speaking, is it correct to say that the difference between webPPL and pymc with regards to this example (or perhaps in general), that webPPL supports the (simple) inference algorithms of exact enumeration and rejection sampling, whereas pymc does not directly support this, so we have to solve this example either with manual rejection sampling or by using the construction with Categorical variables and the lookup table?

7

I am not familiar with the inference method webPPL is using, but the model with Categorical variable also use a reject sampling to do the inference.
In general PyMC does not focus on these type of discrete model as they usually dont scale well.