I would like to have from you an approval or a disapproval for the following method, by which I thought to carry out a prior predictive check, without going through the functions of the ArviZ module.
Note that I’m not trying to find out if the method is really practical, but if it makes sense to do things like that and if it doesn’t contain errors in reasoning.
So, I start from a beta-binomial model (traditional coin-flip model) where the parameter theta is modeled by the prior Beta, say Beta(0.5, 0.5).
I programmed a series of n=73 Bernoulli experiments and my result shows x_{obs}=46 successes. I wonder how could I quantify the fact that my prior is adequate or not.
This article by Coon et al. HERE gives (in its table 2) several “discrepancy functions and pivotal quantities useful for Bayesian model checking” (as quoted), and it seemed useful to me to use the first function (referenced \chi^2), modifying it with a logarithm np.log() so as to reduce excessive variations.
Concretely, for a given \theta parameter, taking into account that the expected number of successes x is n\theta, I calculate the discrepancy value T between a given x (either predicted by sampling or observed) and its expectation, by the formula:
T(x,\theta)=np.log(\frac{(x-n\theta)^2}{n\theta})
My procedure is:
-
to carry out a number N of random draws of the \theta parameter from the prior (say, \theta_i),
-
then, for each \theta_i obtained, to get a number x_i of predicted successes by random draw from the corresponding sampling distribution (i.e. the binomial law Binom(n=73, \theta= \theta_i))
-
and then to apply the discrepancy function T to the (random) value x_i \rightarrow T(x_i, \theta_i) and to the (fixed) value x_{obs} \rightarrow T(x_{obs}, \theta_i) .
This gives me N couples (T(x_i, \theta_i), T(x_{obs}, \theta_i)), for each of which I express the Boolean result (T(x_{obs}, \theta_i) > T(x_i, \theta_i)) as 0 (False) or 1 (True).
Now, the proportion of 1 should give me an approximate value of the probability p that the observed data lie beyond the predicted data.
And, as far as I understand from the usual rules, the model is fit if p\sim0.5 and misfit if p\sim0 or p\sim1 …
The program I used to do so is:
fixing the number of Bernoulli trials
n = 73
fixing the number of observed successes during the trial
x_obs = 46
fixing the parameters of the beta prior
alpha, beta = 0.5, 0.5
fixing the number of draws
draws = 20000
sampling parameter values (\theta) from the prior
thetas = np.random.beta(alpha, beta, size = draws).tolist()
sampling successes x from the likelihood (with the given sampled \theta)
predicted = [np.random.binomial(n, theta, size = 1)[0] for theta in thetas]
expected values from the given likelihood (binomial distribution)
expected = [theta*n for theta in thetas]
assess discrepancies T (through \log(chi^2) computation) for predicted x
T_predicted = [np.log((x - y)**2 / y) for (x, y) in zip(predicted, expected)]
assess discrepancies T (through \log(chi^2) computation) for observed x_{obs}
T_observed = [np.log((x_obs - y)**2 / y) for y in expected]
check when T_observed > T_predicted
checks = [x > y for (x, y) in zip(T_observed, T_predicted)]
other statistics
mean_T_predicted = sum(T_predicted)/len(T_predicted)
mean_T_observed = sum(T_observed)/len(T_observed)prob = sum(checks)/len(checks)
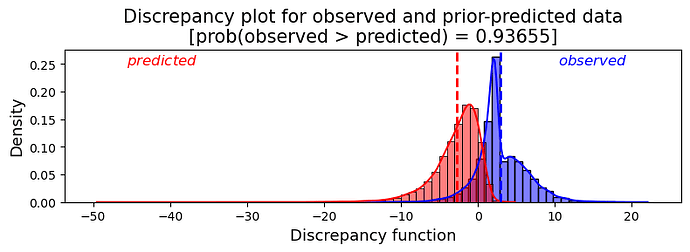
Plotting the N values of the calculated discrepancy function gives me:
I think the plot shows a characteristic pattern of a misfit model. The p-value calculated, which of course varies each time the program is restarted, was 0.93655 in my own run, which confirms, if this procedure is indeed valid, that the model is inadequate, leading to the conclusion that I should change my prior.
I’m sorry it took a bit long to explain… Do you agree with all this ? Do you have any comments (deeply appreciated)?