Mass matrix contains zeros on the diagonal for messy data

Questions
1

This is a relatively simple question. I’ve had no issues working with generated distributions, or any kind of “toy data”, but now that I have attempted to use some real world data that is a bit more messy I am having issues.

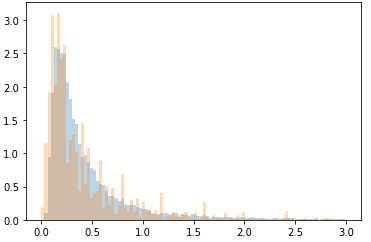
Here is the real data
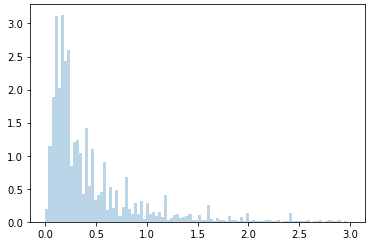
image

Here is the data I generating using a best fit inverse Gaussian distribution
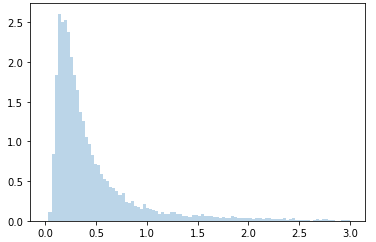
image

I am successful in imputing missing values from the generated data as follows:

with pm.Model() as model:
    
    initial = np.random.randn(ma.count_masked(test)).astype('float64')
    #init = np.abs(np.random.randn(14990,1))
    
    alpha_m=pm.HalfNormal('alpha_m',1,testval=1)
    beta_m=pm.HalfNormal('beta_m',1,testval=1)
    mu_m=pm.Normal('mu_m',0,1,testval=0)
    x = pm.InverseGamma('x',alpha=alpha_m,beta=beta_m,mu=mu_m,observed=data
    approx=pm.sample(2000,tune=2000,progressbar=True,chains=1,init='adapt_diag',target_accept=.99,discard_tuned_samples=True)

image
image867×580 94 KB

However, when using the “real world” data set the sampling fails immediately with the "Mass matrix contains zeros on the diagonal. " error. I’ve tried changing the priors, changing the sampling technique, and quite a few other things but I am at a loss. Is there something I am missing in terms of sampling from a messy distribution like this?

2

As the data is IID I don’t think you get any benefit by imputing missing values. Also, is the real data more noisy? You could do a prior predictive check and see if that matches with the real data at all.

3

Thank you for the response. As far as the data being IDD, agreed, but this is a part of a larger problem I am trying to solve where this will in fact make a difference. Yes, the real data is quite a bit more noisy. Even if I set the priors to be as informative as possible, to the point where I am almost pre-specifying what they should be I still get the same error. Here is the result of that prior predictive check with blue being the prior predictive and the orange being the true noisy data.

image

4

Maybe the likelihood is too unforgiving. You could try a Lognormal, or even better a LogStudentT (which doesn’t exist but if you do a pm.Bound you should be able to create one, however, it might not then work with an observed anymore, but give that a try).

5

Thank you, I will give it a try!