New user of PyMC here! I’m attempting to sample a mixture model that is marginalized over the categorical membership of each data point. For example, given some independent data x, observed values y, models M_i, and model parameters \theta_i, the likelihood is
where q_i is the Dirichlet membership prior. I’ve set up a minimum working example, which is trying to generate the slopes and intercepts of two lines (M_i(x, m_i, b_i) = m_i x + b_i):
import numpy as np
np.random.seed(1234)
import pymc3 as pm
num_data = 1000
xdata = np.random.uniform(0.0, 10.0, num_data)
obs = np.zeros(num_data)
model = np.random.choice([0, 1], p=[0.75, 0.25], size=num_data)
m_trues = np.array([6.0, 2.0])
b_trues = np.array([-12.0, 8.0])
sigma = 1.0
obs[model == 0] = m_trues[0]*xdata[model == 0] + b_trues[0]
obs[model == 1] = m_trues[1]*xdata[model == 1] + b_trues[1]
obs += np.random.randn(num_data)*sigma

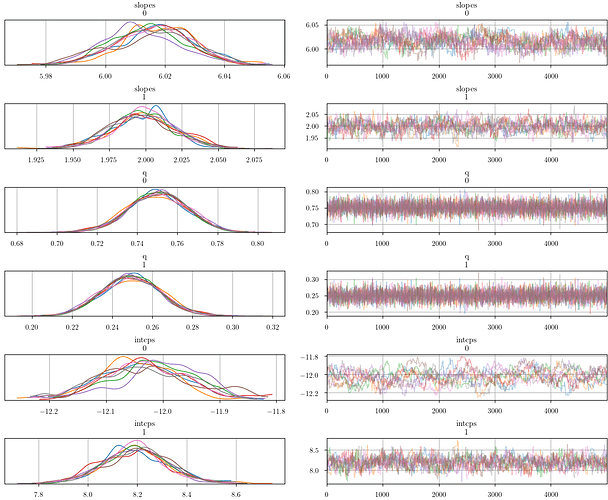
Using Metropolis steps to sample the posterior, I get reasonable results (i.e., the chains converge to the expected values):
with pm.Model() as model:
p = pm.Dirichlet('q', a=np.ones(2))
slopes = pm.Normal('slopes', mu=0.0, sigma=10.0, shape=2, testval=[0.0, 0.0])
intcps = pm.Normal('intcps', mu=0.0, sigma=25.0, shape=2, testval=[-10.0, 10.0], transform=pm.transforms.Ordered())
mus = slopes * xdata[:, np.newaxis] + intcps
like = pm.NormalMixture('like', w=p, mu=mus, sigma=sigma, observed=obs)
with model:
step = pm.Metropolis()
trace = pm.sample(5000, step=step, tune=1000, cores=8)
But, with NUTS, I get unreasonable results (i.e., the chains converge, but not to the expected values):
with model:
step = pm.NUTS()
trace = pm.sample(5000, step=step, tune=1000, cores=8)
Is there something simple that I’m missing? Thanks in advance for your help.