Modeling reinforcement learning of human participant using PyMC3

Maria · August 14, 2018, 10:55pm

Thanks for the help so far with this model!

I am fitting a reinforcement learning model to human behavior in a hierarchical learning task. The model selects actions based on action values (Q-values), which are calculated from trial-by-trial reward prediction errors (RPEs) based on action feedback.

The data can be found here.

import pymc3 as pm
import theano
import theano.tensor as T

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np


# Sampling
n_samples = 100
n_tune = 50
n_cores = 1
n_chains = 1

# Get data
n_seasons, n_TS, n_aliens, n_actions = 3, 3, 4, 3
n_trials, n_subj = 440, 31
alien_initial_Q = 0.12
seasons = T.as_tensor_variable(pd.read_csv("seasons.csv"))  # stimulus part 1
aliens = T.as_tensor_variable(pd.read_csv("aliens.csv"))  # stimulus part 2
actions = T.as_tensor_variable(pd.read_csv("actions.csv"))  # participants' selected actions
rewards = T.as_tensor_variable(pd.read_csv("rewards.csv"))  # participants' received rewards

trials, subj = np.meshgrid(range(n_trials), range(n_subj))
trials = T.as_tensor_variable(trials.T)
subj = T.as_tensor_variable(subj.T)

# Fit model
with pm.Model() as model:

    # RL parameters: softmax temperature beta; learning rate alpha; Q-value forgetting
    beta_mu = pm.Uniform('beta_mu', lower=0, upper=5, testval=1.25)
    beta_sd = pm.Uniform('beta_sd', lower=0, upper=5, testval=0.1)
    beta_matt = pm.Normal('beta_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-0.1, 0, 0.1], n_subj))
    beta = pm.Deterministic('beta', beta_mu + beta_sd * beta_matt)

    alpha_mu = pm.Uniform('alpha_mu', lower=0, upper=1, testval=0.15)
    alpha_sd = pm.Uniform('alpha_sd', lower=0, upper=1, testval=0.05)
    alpha_matt = pm.Normal('alpha_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-1, 0, 1], n_subj))
    alpha = pm.Deterministic('alpha', alpha_mu + alpha_sd * alpha_matt)

    forget_mu = pm.Uniform('forget_mu', lower=0, upper=1, testval=0.06)
    forget_sd = pm.Uniform('forget_sd', lower=0, upper=1, testval=0.03)
    forget_matt = pm.Normal('forget_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-1, 0, 1], n_subj))
    forget = pm.Deterministic('forget', forget_mu + forget_sd * forget_matt)

    # Get the right shapes
    betas = T.tile(T.repeat(beta, n_actions), n_trials).reshape([n_trials, n_subj, n_actions])    # Q_sub.shape
    forgets = T.repeat(forget, n_TS * n_aliens * n_actions).reshape([n_subj, n_TS, n_aliens, n_actions])  # Q_low for 1 trial

    # Initialize Q-values
    Q_low0 = alien_initial_Q * T.ones([n_subj, n_TS, n_aliens, n_actions])

    # Update Q-values based on stimulus, action, and reward
    def update_Qs(season, alien, action, reward, Q_low, alpha, forget, n_subj):
        # Loop over trials: take data for all subjects, 1 single trial

        # Forget Q-values a little bit in each trial
        Q_low_new = (1 - forget) * Q_low + forget * alien_initial_Q * T.ones_like(Q_low)

        # Calculate RPE & update Q-values
        RPE_low = reward - Q_low_new[T.arange(n_subj), season, alien, action]
        Q_low_new = T.set_subtensor(Q_low_new[T.arange(n_subj), season, alien, action],
                                    Q_low_new[T.arange(n_subj), season, alien, action] + alpha * RPE_low)

        return Q_low_new


    # Get Q-values for the whole task (update Q-values in each trial)
    Q_low, _ = theano.scan(fn=update_Qs,
                           sequences=[seasons, aliens, actions, rewards],
                           outputs_info=[Q_low0],
                           non_sequences=[alpha, forgets, n_subj])

    Q_low = T.concatenate([[Q_low0], Q_low[:-1]], axis=0)  # Add first trial's Q-values, remove last trials Q-values
    T.printing.Print("Q_low")(Q_low)

    # Subset Q-values according to stimuli and responses in each trial
    Q_sub = Q_low[trials, subj, seasons, aliens]

    # First step to translate into probabilities: apply exp
    p = T.exp(betas * Q_sub)

    # Bring p in the correct shape for pm.Categorical: 2-d array of trials
    action_wise_p = p.reshape([n_trials * n_subj, n_actions])
    action_wise_actions = actions.flatten()

    # Select actions (& second step of calculating probabilities: normalize)
    actions = pm.Categorical('actions', p=action_wise_p, observed=action_wise_actions)

    # Sample the model
    trace = pm.sample(n_samples, tune=n_tune, chains=n_chains, cores=n_cores, nuts_kwargs=dict(target_accept=.80))

pm.traceplot(trace)
plt.savefig('trace_plot.png')
model_summary = pm.summary(trace)
pd.DataFrame(model_summary).to_csv('model_summary.csv')

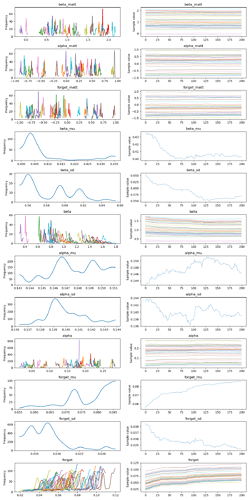
The traceplot looks like this, which seems reasonable given the small number of sampling steps. The values of alpha, beta, and forget make absolute sense for the task:

I don’t have a lot of experience using PyMC3. Does the model and the results look reasonable so far?

What I would like to do next, and where I am running into problems, is adding hierarchy to the RL model. Currently, the model stores the Q-values separately for each season-alien-action compound. What I would like to do instead is to learn the Q-values for each season inside a separate “task set” (TS).

Here is my attempt for modeling (the main difference is within update_Qs):

import pymc3 as pm
import theano
import theano.tensor as T

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np


# Sampling
n_samples = 200
n_tune = 50
n_cores = 1
n_chains = 1

# Get data
n_seasons, n_TS, n_aliens, n_actions = 3, 3, 4, 3
n_trials, n_subj = 440, 31
alien_initial_Q = 0.12
seasons = T.as_tensor_variable(pd.read_csv("seasons.csv"))
aliens = T.as_tensor_variable(pd.read_csv("aliens.csv"))
actions = T.as_tensor_variable(pd.read_csv("actions.csv"))
rewards = T.as_tensor_variable(pd.read_csv("rewards.csv"))

trials, subj = np.meshgrid(range(n_trials), range(n_subj))
trials = T.as_tensor_variable(trials.T)
subj = T.as_tensor_variable(subj.T)

# Fit model
with pm.Model() as model:

    # RL parameters: softmax temperature beta; learning rate alpha; Q-value forgetting
    beta_mu = pm.Uniform('beta_mu', lower=0, upper=5, testval=1.25)
    beta_sd = pm.Uniform('beta_sd', lower=0, upper=5, testval=0.1)
    beta_matt = pm.Normal('beta_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-0.1, 0, 0.1], n_subj))
    beta = pm.Deterministic('beta', beta_mu + beta_sd * beta_matt)

    alpha_mu = pm.Uniform('alpha_mu', lower=0, upper=1, testval=0.15)
    alpha_sd = pm.Uniform('alpha_sd', lower=0, upper=1, testval=0.05)
    alpha_matt = pm.Normal('alpha_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-1, 0, 1], n_subj))
    alpha = pm.Deterministic('alpha', alpha_mu + alpha_sd * alpha_matt)

    forget_mu = pm.Uniform('forget_mu', lower=0, upper=1, testval=0.06)
    forget_sd = pm.Uniform('forget_sd', lower=0, upper=1, testval=0.03)
    forget_matt = pm.Normal('forget_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-1, 0, 1], n_subj))
    forget = pm.Deterministic('forget', forget_mu + forget_sd * forget_matt)

    beta_high = beta.copy()
    alpha_high = alpha.copy()
    forget_high = forget.copy()

    # Get the right shapes
    betas = T.tile(T.repeat(beta, n_actions), n_trials).reshape([n_trials, n_subj, n_actions])    # Q_sub.shape
    beta_highs = T.repeat(beta_high, n_TS).reshape([n_subj, n_TS])  # Q_high_sub.shape

    forgets = T.repeat(forget, n_TS * n_aliens * n_actions).reshape([n_subj, n_TS, n_aliens, n_actions])  # Q_low for 1 trial
    forget_highs = T.repeat(forget_high, n_seasons * n_TS).reshape([n_subj, n_seasons, n_TS])  # Q_high for 1 trial

    # Initialize Q-values
    Q_low0 = alien_initial_Q * T.ones([n_subj, n_TS, n_aliens, n_actions])
    Q_high0 = alien_initial_Q * T.ones([n_subj, n_seasons, n_TS])

    # Update Q-values based on stimulus, action, and reward
    def update_Qs(season, alien, action, reward, Q_low, Q_high, alpha, alpha_high, beta_high, forget, forget_high,
                  n_subj):
        # Loop over trials: take data for all subjects, 1 single trial

        # Select TS
        Q_high_sub = Q_high[T.arange(n_subj), season]
        p_high = T.exp(beta_high * Q_high_sub)
        # TS = season  # Use this line instead of the next one to get similar results as for the flat model above
        TS = p_high.argmax(axis=1)  # Select one TS deterministically

        # Forget Q-values a little bit
        Q_low_new = (1 - forget) * Q_low + forget * alien_initial_Q * T.ones_like(Q_low)
        Q_high_new = (1 - forget_high) * Q_high + forget_high * alien_initial_Q * T.ones_like(Q_high)

        # Calculate RPEs & update Q-values
        RPE_low = reward - Q_low_new[T.arange(n_subj), TS, alien, action]
        Q_low_new = T.set_subtensor(Q_low_new[T.arange(n_subj), TS, alien, action],
                                    Q_low_new[T.arange(n_subj), TS, alien, action] + alpha * RPE_low)

        RPE_high = reward - Q_high_new[T.arange(n_subj), season, TS]
        Q_high_new = T.set_subtensor(Q_high_new[T.arange(n_subj), season, TS],
                                     Q_high_new[T.arange(n_subj), season, TS] + alpha_high * RPE_high)

        return [Q_low_new, Q_high_new]

    # Get Q-values for the whole task (update each trial)
    [Q_low, Q_high], _ = theano.scan(fn=update_Qs,  # hierarchical: TS = p_high.argmax(axis=1); flat: TS = season
                                     sequences=[seasons, aliens, actions, rewards],
                                     outputs_info=[Q_low0, Q_high0],
                                     non_sequences=[alpha, alpha_high, beta_highs, forgets, forget_highs, n_subj])

    Q_low = T.concatenate([[Q_low0], Q_low[:-1]], axis=0)  # Add first trial's Q-values, remove last trials Q-values
    T.printing.Print("Q_low")(Q_low)
    T.printing.Print("Q_high")(Q_high)

    # Subset Q-values according to stimuli and responses in each trial
    Q_sub = Q_low[trials, subj, seasons, aliens]

    # First step to translate into probabilities: apply exp
    p = T.exp(betas * Q_sub)

    # Bring p in the correct shape for pm.Categorical: 2-d array of trials
    action_wise_p = p.reshape([n_trials * n_subj, n_actions])
    action_wise_actions = actions.flatten()

    # Select actions (& second step of calculating probabilities: normalize)
    actions = pm.Categorical('actions', p=action_wise_p, observed=action_wise_actions)

    # Sample the model
    trace = pm.sample(n_samples, tune=n_tune, chains=n_chains, cores=n_cores, nuts_kwargs=dict(target_accept=.80))

pm.traceplot(trace)
plt.savefig('trace_plot.png')
model_summary = pm.summary(trace)
pd.DataFrame(model_summary).to_csv('model_summary.csv')

Here is the corresponding traceplot:

I have the following questions:

Every now and then, the model doesn’t start sampling because initial energy is bad. Sometimes it works, and sometimes it doesn’t. What could cause this behavior?
The sampler clearly gets stuck. The only difference between the second model and the first is the line TS = p_high.argmax(axis=1). If I replace it with TS = season, the models are identical and the traces look good. Why does this line create sampling problems, and is there a way to fix it?
The model uses an incredible amount of memory (>50 GB for 100 samples in 2 chains) and runs very slowly. Did I introduce a memory leak?

Any thoughts and feedback would be greatly appreciated!

junpenglao · August 19, 2018, 8:09am

A few quick thought:

you should use a softmax instead of doing T.repeat to to expand the weight to a right shape.
the choice of priors are a bit odd to me - is there any reason that you are using Uniform(0, 5) for betas?
I think you want to model forget and alpha to be in [0, 1] right? The current way you are doing might not give you parameter that satisfy such constraint.
maybe the theano.scan part could be rewrite into something doesnt need the scan?

Maria · August 30, 2018, 8:06pm

Hi Junpeng,

Thank you for your thoughts!

I chose better priors for beta, and fixed the ranges for alpha and forget, like you suggested. I was not sure how to use the softmax instead of T.repeat for the weights though, because my matrix is 4d and won’t be accepted by T.nnet.sofmax - or were you thinking about a different softmax function? As for the scan, I don’t think there is a way to get rid of it unfortunately, because each row of Q_sub depends on the previous row, so I need to pass the previous results to new each iteration.

For the priors, I am now using:

beta_mu = pm.Gamma('beta_mu', mu=1, sd=2, testval=1.25)
beta_sd = pm.HalfNormal('beta_sd', sd=0.5, testval=0.1)

alpha_mu = pm.Uniform('alpha_mu', lower=0, upper=1, testval=0.15)
alpha_sd = pm.HalfNormal('alpha_sd', sd=0.1, testval=0.05)

forget_mu = pm.Uniform('forget_mu', lower=0, upper=1, testval=0.06)
forget_sd = pm.HalfNormal('forget_sd', sd=0.1, testval=0.03)

I fixed the ranges of all parameters using pm.Bound on the individual non-central parameters:

beta_matt = pm.Bound(pm.Normal, lower=-beta_mu / beta_sd)(
        'beta_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-1, 0, 1], n_subj))
beta = pm.Deterministic('beta', beta_mu + beta_sd * beta_matt)
    
alpha_matt = pm.Bound(pm.Normal, lower=-alpha_mu / alpha_sd, upper=(1 - alpha_mu) / alpha_sd)(
        'alpha_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-1, 0, 1], n_subj))
alpha = pm.Deterministic('alpha', alpha_mu + alpha_sd * alpha_matt)

forget_matt = pm.Bound(pm.Normal, lower=-forget_mu / forget_sd, upper=(1 - forget_mu) / forget_sd)(
        'forget_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-1, 0, 1], n_subj))
forget = pm.Deterministic('forget', forget_mu + forget_sd * forget_matt)

After these fixes, the results still look the same (excuse the small number of samples).
First, flat model:

Second, hierarchical model:

I am nor sure what to try next. Do you have any ideas?

I also found a great PyMC3 tutorial by Chris Fonnesbeck with a notebook about model checking and will go through it next, to see what else I could check or fix. Do you know of any other resources that could be helpful?

Thanks!

junpenglao · August 30, 2018, 8:26pm

Hi Maria,
I meant to get back to you on this - I actually started to play with the model, and see if there are ways to replace the theano.scan. I also come to the conclusion that it is possibly too difficult, and instead rewrite it slightly so that it doesnt output the whole 4D matrix (in the hope that it would make things faster). Unfortunately it is still pretty slow and the sample doesnt seems to work. Anyway, here is the code https://github.com/junpenglao/Planet_Sakaar_Data_Science/blob/master/PyMC3QnA/discourse_1735.ipynb, hopefully it can give you some inspiration. I suggest try just model 1 or 2 subjects and make sure it works first, as the sampling is too slow

Maria · September 6, 2018, 10:44pm

Hi Junpeng,

Thank you for your suggestions! I managed to integrate a few of them, and my first model seems to be working fine now, well enough for my purposes. (Alpha and beta are correlated in the model, which I think might be a problem, but all RL model have this problem and I hope it’s not crucial.)

Nevertheless, I still have problems with the second version of the model. It is impressive how such a small difference can change so much. I am pretty certain that my model is reasonable because I simulated data from it, and it looks very similar to the empirical data that I am trying to fit, so I am replicating the important patterns. Still, the model either errs with ValueError: Bad initial energy: inf. The model might be misspecified. or, if it runs, it gets stuck immediately:

Here is the code for my model, based on your code (note that this is a .ipynb file, I just changed the extension to .txt to be able to upload it here): discourse_1735.txt (13.7 KB)

Maria · September 26, 2018, 6:55am

This is a a follow-up for other people who might run into similar issues.

I finally got my models to run. What did the trick was the combination of a few things: I picked better, i.e., much more informative priors, fixed a bug in the update function, found a way around explicit sampling inside the theano.scan loop, and basically deconstructed and then reconstructed the whole model, starting by removing all group-level parameters, the non-centered implementation, throwing out all unnecessary parameters, starting with the simplest model possible, and then working my way up toward more complex models step by step.

What also helped me a lot was writing a simulation script in parallel that created data based on a model identical to the one I was implementing in PyMC3. Simulating data gave me an idea of whether my model was able to capture the interesting effects in my data at all, and fitting my model to simulated data showed me how well my model was recovering parameters in a best-case scenario.

With that, here is some data (30 softmax TS agents):
rewards.csv (64.0 KB)
seasons.csv (26.3 KB)
actions.csv (26.3 KB)
aliens.csv (26.3 KB)

Here are the parameters that were used to simulate the data:
true_params.csv (3.6 KB)

And here is the working model: https://github.com/MariaEckstein/SLCN/blob/master/models/discourse_1735_fixed.ipynb

(For an unknown reason, the jupyter version of the script won’t allow me to define my forget and forget_high parameters based on pm.Beta distributions, so I replaced them with pm.HalfNormal. The commented-out lines are the ones that should be run though.)

I’m still looking for any kind of feedback, so I’d be happy to hear all thoughts and ideas!

junpenglao · September 26, 2018, 7:37am

To me your workflow is great! This is a perfect example of the box-loop and bayesian workflow. You should write a blog post of the things you have tried.

ruyuanzhang · June 3, 2023, 3:19pm

Maria:

import pymc3 as pm
import theano
import theano.tensor as T

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np


# Sampling
n_samples = 200
n_tune = 50
n_cores = 1
n_chains = 1

# Get data
n_seasons, n_TS, n_aliens, n_actions = 3, 3, 4, 3
n_trials, n_subj = 440, 31
alien_initial_Q = 0.12
seasons = T.as_tensor_variable(pd.read_csv("seasons.csv"))
aliens = T.as_tensor_variable(pd.read_csv("aliens.csv"))
actions = T.as_tensor_variable(pd.read_csv("actions.csv"))
rewards = T.as_tensor_variable(pd.read_csv("rewards.csv"))

trials, subj = np.meshgrid(range(n_trials), range(n_subj))
trials = T.as_tensor_variable(trials.T)
subj = T.as_tensor_variable(subj.T)

# Fit model
with pm.Model() as model:

    # RL parameters: softmax temperature beta; learning rate alpha; Q-value forgetting
    beta_mu = pm.Uniform('beta_mu', lower=0, upper=5, testval=1.25)
    beta_sd = pm.Uniform('beta_sd', lower=0, upper=5, testval=0.1)
    beta_matt = pm.Normal('beta_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-0.1, 0, 0.1], n_subj))
    beta = pm.Deterministic('beta', beta_mu + beta_sd * beta_matt)

    alpha_mu = pm.Uniform('alpha_mu', lower=0, upper=1, testval=0.15)
    alpha_sd = pm.Uniform('alpha_sd', lower=0, upper=1, testval=0.05)
    alpha_matt = pm.Normal('alpha_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-1, 0, 1], n_subj))
    alpha = pm.Deterministic('alpha', alpha_mu + alpha_sd * alpha_matt)

    forget_mu = pm.Uniform('forget_mu', lower=0, upper=1, testval=0.06)
    forget_sd = pm.Uniform('forget_sd', lower=0, upper=1, testval=0.03)
    forget_matt = pm.Normal('forget_matt', mu=0, sd=1, shape=n_subj, testval=np.random.choice([-1, 0, 1], n_subj))
    forget = pm.Deterministic('forget', forget_mu + forget_sd * forget_matt)

    beta_high = beta.copy()
    alpha_high = alpha.copy()
    forget_high = forget.copy()

    # Get the right shapes
    betas = T.tile(T.repeat(beta, n_actions), n_trials).reshape([n_trials, n_subj, n_actions])    # Q_sub.shape
    beta_highs = T.repeat(beta_high, n_TS).reshape([n_subj, n_TS])  # Q_high_sub.shape

    forgets = T.repeat(forget, n_TS * n_aliens * n_actions).reshape([n_subj, n_TS, n_aliens, n_actions])  # Q_low for 1 trial
    forget_highs = T.repeat(forget_high, n_seasons * n_TS).reshape([n_subj, n_seasons, n_TS])  # Q_high for 1 trial

    # Initialize Q-values
    Q_low0 = alien_initial_Q * T.ones([n_subj, n_TS, n_aliens, n_actions])
    Q_high0 = alien_initial_Q * T.ones([n_subj, n_seasons, n_TS])

    # Update Q-values based on stimulus, action, and reward
    def update_Qs(season, alien, action, reward, Q_low, Q_high, alpha, alpha_high, beta_high, forget, forget_high,
                  n_subj):
        # Loop over trials: take data for all subjects, 1 single trial

        # Select TS
        Q_high_sub = Q_high[T.arange(n_subj), season]
        p_high = T.exp(beta_high * Q_high_sub)
        # TS = season  # Use this line instead of the next one to get similar results as for the flat model above
        TS = p_high.argmax(axis=1)  # Select one TS deterministically

        # Forget Q-values a little bit
        Q_low_new = (1 - forget) * Q_low + forget * alien_initial_Q * T.ones_like(Q_low)
        Q_high_new = (1 - forget_high) * Q_high + forget_high * alien_initial_Q * T.ones_like(Q_high)

        # Calculate RPEs & update Q-values
        RPE_low = reward - Q_low_new[T.arange(n_subj), TS, alien, action]
        Q_low_new = T.set_subtensor(Q_low_new[T.arange(n_subj), TS, alien, action],
                                    Q_low_new[T.arange(n_subj), TS, alien, action] + alpha * RPE_low)

        RPE_high = reward - Q_high_new[T.arange(n_subj), season, TS]
        Q_high_new = T.set_subtensor(Q_high_new[T.arange(n_subj), season, TS],
                                     Q_high_new[T.arange(n_subj), season, TS] + alpha_high * RPE_high)

        return [Q_low_new, Q_high_new]

    # Get Q-values for the whole task (update each trial)
    [Q_low, Q_high], _ = theano.scan(fn=update_Qs,  # hierarchical: TS = p_high.argmax(axis=1); flat: TS = season
                                     sequences=[seasons, aliens, actions, rewards],
                                     outputs_info=[Q_low0, Q_high0],
                                     non_sequences=[alpha, alpha_high, beta_highs, forgets, forget_highs, n_subj])

    Q_low = T.concatenate([[Q_low0], Q_low[:-1]], axis=0)  # Add first trial's Q-values, remove last trials Q-values
    T.printing.Print("Q_low")(Q_low)
    T.printing.Print("Q_high")(Q_high)

    # Subset Q-values according to stimuli and responses in each trial
    Q_sub = Q_low[trials, subj, seasons, aliens]

    # First step to translate into probabilities: apply exp
    p = T.exp(betas * Q_sub)

    # Bring p in the correct shape for pm.Categorical: 2-d array of trials
    action_wise_p = p.reshape([n_trials * n_subj, n_actions])
    action_wise_actions = actions.flatten()

    # Select actions (& second step of calculating probabilities: normalize)
    actions = pm.Categorical('actions', p=action_wise_p, observed=action_wise_actions)

    # Sample the model
    trace = pm.sample(n_samples, tune=n_tune, chains=n_chains, cores=n_cores, nuts_kwargs=dict(target_accept=.80))

pm.traceplot(trace)
plt.savefig('trace_plot.png')
model_summary = pm.summary(trace)
pd.DataFrame(model_summary).to_csv('model_summary.csv')

@Maria Hi, Maria, it seems the link of the working model is broken. Can you reshare the working model for us?? Thanks a buntch.

@junpenglao Hi, junpeng. We are doing the similar hierarchical reinforcement learning model. I understand we should use scan to loop across trials but we still need to loop across different subjects? can I use a scan within another scan??? and typically how to best deal with two for loop??? Thanks

orduek · June 7, 2023, 11:50am

This might be helpful.

https://github.com/orduek/aversive_learning_simulation

Topic		Replies	Views
Fitting Reinforcement Learning model modeling	0	246	November 4, 2023
Some questions about PyMC Models in online settings v5	3	311	August 29, 2023
Parameter Learning in Simple Bayesian Network Questions	5	2678	April 2, 2018
Help with Hierarchical Model Example Questions	3	370	October 5, 2021
Modeling an agent whose actions depend on expected value of future actions (Updated Question) version agnostic modeling	2	493	May 17, 2023

Modeling reinforcement learning of human participant using PyMC3

Related Topics