New sampling algorithm from a MCMC newbie

1

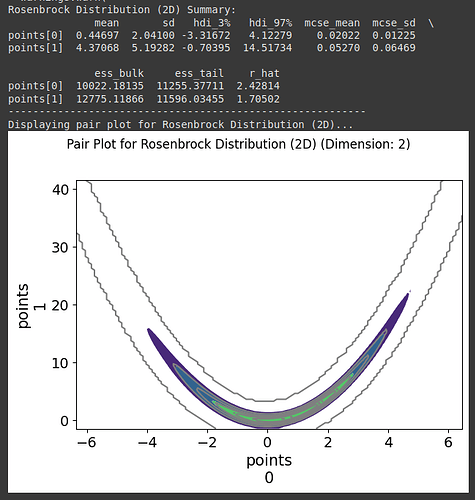
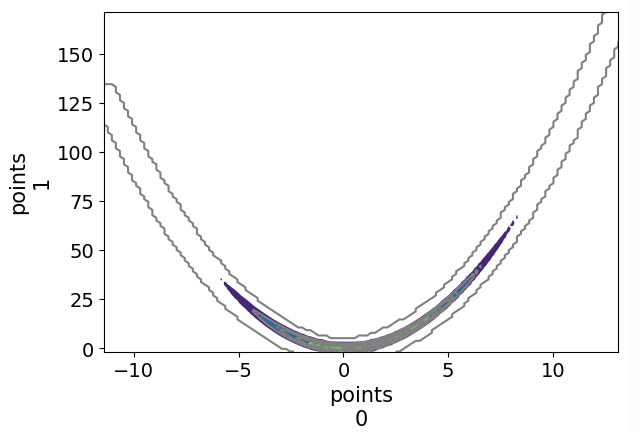
Hello !

Last weekend I watched this video about diffusion models and learned about Langevin diffusion.

(I am originally a C++ dev who is now doing a bit of python/pytorch)

This first seemed crazy to me that a random walk combined with a gradient descent on the log potential could get you this very potential (with the subtle sqrt(eps/2) mix) so I had to look into the proofs and I also had an idea about combining optimizer algorithm with Langevin diffusion.

The idea is pretty simple and after coding it up I found a paper from 2020 doing exactly what I did.

Then I learned about MALA, HMC and NUTS (this Hamiltonian idea is incredible) and I had an other idea for a sampler.

The issue with discretize langevin stepsize is you get some kind of convolution by a gaussian kernel of the posterior you are trying to sample. You can reduce the stepsize but you get much more autocorrelation.

My idea was to:

  • use many // chains using the modern vectorized hardware that we have
  • use adaptative gradients scheme as warmup since it would explore much faster
  • use subchains with a (1-t)^2 annealing schedule after warmup keeping only the last subchain sample

edit: the schedule idea is very similar to this paper I’m always 5/6 years late…

This way you progressively deacrease the variance of the noise kernel, get your sample and start again from large variance noise kernel. Since you go from enlarge fuzzy density to a much sharper image, it looks like a “vascularisation” of the distribution, hence the codename for this sampling algorithm: Hearbeat.

I wrote the sampler in pytorch and asked Gemini to recode it in JAX (got a x3 speed improvement) and I’ve tried running the sampler on a very simple mixture of gaussian against other JAX samplers from PyMC (numpyro and blackjax), and I get very comparable result for a very different algorithm. ^^ (note I used 1024 chains for my algo and 8 for the NUTS sampler to get similar running time, 8 chains seems to get the fastest ESS/sec for the NUTS samplers)

I ran on CPU without multithread and need to do much more tests with other distributions and on GPU. From what I get, it is much easier to tune my sampler to increase num_sample/ESS where for example the acceptance probability isn’t ideal for NUTS. It is also much much faster on CPU than NUTS sampler if you need many chains, I need to check this is also the case on GPU.

It is way too early to share but I’m too excited not to so here is a notebook if you want to play with it. I will see if I can provide a better support (colab?) later this we. Any comments are welcome. :slight_smile:

Colab link: Google Colab

Thank you for reading this far.

NB: Beware I am not a statistician and still very new to bayesian statistics.

2 Likes
2

Not sure why I cannot edit my post anymore but I ran it on 8 TPUv2 and get ~60k ESS/s with a ESS/num_samples > 0.99.

HeartBeat Summary:
              mean       sd   hdi_3%  hdi_97%  mcse_mean  mcse_sd  \
points[0]  1.20289  1.99133 -1.86957  5.21001    0.00138  0.00097   
points[1]  0.80211  1.72083 -2.38160  4.02596    0.00119  0.00080   

               ess_bulk      ess_tail    r_hat  
points[0]  2.082956e+06  2.091615e+06  1.00001  
points[1]  2.087530e+06  2.092678e+06  1.00003

The x/y-variances and y-mean are within the 95% credible interval (if I am not mistaken) but the x-mean falls very close with a p-value of 4%. I am pretty sure there is bias from the annealing which you can alleviate with longer subchains/leaps (increasing num_steps) lowering ESS/sec but I think this kind of bias is acceptable in practice.

I should use some more complicated posterior than my 2D gaussian mixture in the future.

I did manage to make numpyro nuts sampler work on TPUs but it was so slow there must be something wrong (2min for 4 chains of 2048 samples) so I cannot do a comparison. Blackjax is the same. Will need to check on GPU (even discounting the initial model compilation).