Sampling from nested models

Questions
1

Say we generate data by nesting a latent variable from a logistic model within a Poisson model (perhaps “nesting” is not the best word here, but I do not know a better one). For example:

import pymc3 as pm
import numpy as np

# generate data
rng = np.random.default_rng(12345678)

# Parameters of interest
a = 0.9
b = -0.7
c = -0.3
d = 0.5
x_1 = rng.random(1000)
# Latent is the logistic reg. latent variable
latent = a + x_1*b
p = 1/(1+np.exp(-latent))
# observed trials
trial_success = np.int_( rng.random(x_1.shape[0]) < p)
# Now the number of events
lam = np.exp(c + d*latent)
num_event = rng.poisson(lam=lam)

Intuitively, the way I would model this is to nest a logistic regression inside a Poisson model:

# Now both at the same time
with pm.Model() as simple_log:
    a_ = pm.Normal('a', 0, sd=100)
    b_ = pm.Normal('b', 0, sd=100)
    c_ = pm.Normal('c', 0, sd=100)
    d_ = pm.Normal('d', 0, sd=100)
    # Latent specification
    # Latent for the bernoulli
    latent_ = pm.Deterministic(name='latent_bin', var= a_ + b_ * x_1)
    # Latent for the poisson
    latent_2 = pm.Deterministic(name='latent_pois', var=c_ + latent_*d_ )
    # Bernoulli random vector with probability of success
    pm.Bernoulli(name='logit', p=pm.invlogit(latent_), observed=trial_success)
    # Poisson random vector
    pm.Poisson(name='pois', mu=pm.math.exp(latent_2), observed=numbers)

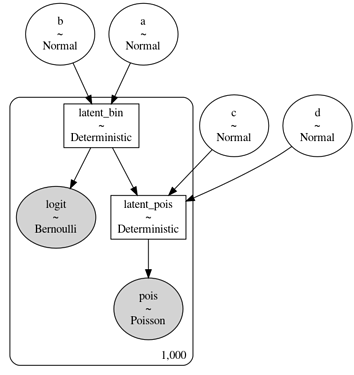
This is the DAG of the model, which corresponds to the generating process above (as far as I can understand):

Digraph.gv
Digraph.gv574×606 17.5 KB

However, I am having a really hard time to sample from this model, as I anticipated. Is there a good way to re-parametrize the model – or any miraculous receipt for sampling?

To stabilize sampling, I can think about ways to independently sample the logistic and Poisson part of the model. First, I can fit a standard logistic regression. Then, if I fix the a and b parameters to their posterior expected value in the Poisson part, the Poisson part becomes a standard GLM again. Yet, if I fix the a and b parameters, I am losing all information about the variability in my posteriors. So I am wondering if there is any way to incorporate that information.

2 Likes
2

What problems are you seeing?

3

All the signs of non-convergence you can get, starting from a very slow sampling:

with simple_log:
    log_trace = pm.sample(4000, chains=3, tune=1000, random_seed=101010, return_inferencedata=True, target_accept=0.9)

Output:

Sampling 3 chains for 1_000 tune and 4_000 draw iterations (3_000 + 12_000 draws total) took 750 seconds.
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
There were 9 divergences after tuning. Increase `target_accept` or reparameterize.
The acceptance probability does not match the target. It is 0.8152433470462593, but should be close to 0.9. Try to increase the number of tuning steps.
There were 4 divergences after tuning. Increase `target_accept` or reparameterize.
The chain reached the maximum tree depth. Increase max_treedepth, increase target_accept or reparameterize.
The rhat statistic is larger than 1.4 for some parameters. The sampler did not converge

The sampling is clearly biased – or very slow to mix. For example the d parameter has an expected posterior of -13 (should be 0.5).

4

Your priors also look a bit too broad.

Other than that you might have some redundancy going on in your linear models, I would try to set some of the intercepts / coefficients to the true values and see if it samples better, to identify the culprits.

Can you show some trace plots and pairwise correlation plots of the posterior parameters?

1 Like
5

I have never seen such bad plots :slight_smile:

trace
trace1200×800 203 KB

pairwise
pairwise1848×977 65.9 KB

I would conclude that yes, the sample does not converge in the right region. The pairwise plot shows that the parameters are really correlated. In particular d, c and b (well, 3 out of 4).

6

It seems that the latent does not vary enough to inform the lam parameter. In particular you can reverse c and d and get basically the same lam parameter

sns.kdeplot(c + latent * d)
sns.kdeplot(-c + latent * (-d))

image

7

Agreed, but I do not understand why. latent_ shouldn’t be that uninformative, it has variation…
In any case, 1. this is screaming for re-parametrization (but I would not know how, exactly) and 2. I will follow your advice to fix some parameters to see if it gets better.

8

Not enough variation for this model, it seems. It spans the range 0.2 - 0.9 which is not much for a Poisson GLM with uninformative priors (and / or this dataset size / coefficient ranges).

9

So you think that if I had more variation in the latent_ variables the model should be fine?

10

I think so. Here I increased the variance of x_1 by a factor of 4 and it seems to sample just fine: Google Colaboratory

Now you might be unlucky in that your data actually looks like your original parameters, in which case you might need a simpler model (or much more regularization)

11

You are right that sampling looks much better with more variability. Thanks for all your help with this.