Hi,
General problem statement – I’m trying to predict terminal conversion rates for cohorts that take a while to mature based on their data “so far”. To do so, I’m using a Beta distribution to characterize the typical conversion rates over an observed bernoulli distribution of the conversion rates so far for the cohort.
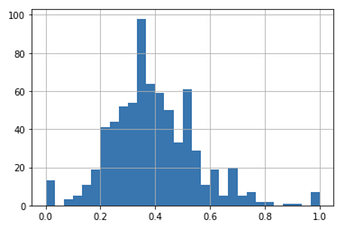
Here is what a typical conversion rate distribution looks like for a given cohort and step in my process:
Naturally, those peaks at 0 and 1 cause issues when I use a beta alone. I attempted to follow an existing thread here, and arrived at the following code where historic_a and _b are found using scipy to fit a beta to the non 0 or 1 historical conversion rates:
test_obs_data = sp.stats.bernoulli.rvs(0.33, 200)
epsilon = 1e-3
historic_a = 9
historic_b = 75
with pm.Model() as model:
mixture_beta = pm.Beta.dist(historic_a, historic_b)
u_0 = pm.Uniform.dist(0, epsilon)
u_1 = pm.Uniform.dist(1-epsilon, 1)
p = pm.Beta('p', 1, 1, shape=2)
dists = [u_0, u_1, mixture_beta]
weights = [p[0], (1-p[0])*p[1], (1-p[0])*(1-p[1])]
mixture = pm.Mixture('mixture', w=weights, comp_dists=dists)
obs = pm.Bernoulli('obs', mixture, observed=test_obs_data)
trace = pm.sample(2000)
The above code results in an error:
AttributeError: Can't pickle local object 'Mixture._comp_dist_random_wrapper.<locals>.wrapped_random'
What am I doing wrong?
I didn’t get the same error was you when I ran just the code block shown. I did, however, get a bad energy error because test_obs_data didn’t generate bernoulli RVs. Try replacing it with the following line:
test_obs_data = (np.random.uniform(size=200) > 0.33).astype(int)
Then, the code should run. I finished sampling with no errors.
Thanks for having a look. I replaced my test_obs_data with your code, but I’m still getting the same error. I also did a pip install --upgrade pymc3 without luck. What else could be causing this issue?
test_obs_data = (np.random.uniform(size=200) > 0.33).astype(int)
epsilon = 1e-3
historic_a = 9
historic_b = 75
with pm.Model() as model:
mixture_beta = pm.Beta.dist(historic_a, historic_b)
u_0 = pm.Uniform.dist(0, epsilon)
u_1 = pm.Uniform.dist(1-epsilon, 1)
p = pm.Beta('p', 1, 1, shape=2)
dists = [u_0, u_1, mixture_beta]
weights = [p[0], (1-p[0])*p[1], (1-p[0])*(1-p[1])]
mixture = pm.Mixture('mixture', w=weights, comp_dists=dists)
obs = pm.Bernoulli('obs', mixture, observed=test_obs_data)
trace = pm.sample(2000)
AttributeError: Can't pickle local object 'Mixture._comp_dist_random_wrapper.<locals>.wrapped_random'
Could you try sampling with trace = pm.sample(2000, cores=1, chains=1) ?
Thank you, that worked! However, the results are not what I’d expect (see below). Why don’t I see a bump in mixture around the 0.33 mark instead of at 0.5?
I tried adjusting your values for historic_a and historic_b and found that the sampler wouldn’t work for more uninformative parameter values. This suggests to me that the nature of the prior here is probably an issue.
My gut feeling on this is that there is a more compact way to pull in the prior information regarding 0-1 inflation into the Beta prior. To go way out on a limb here, I think that simply adding the 0-counts to the first parameter and the 1-counts to the second parameter of your beta component will produce a beta distribution with similar properties to the marginal mixture distribution over p that you’re interested in. Apologies if this description is unhelpful.
1 Like