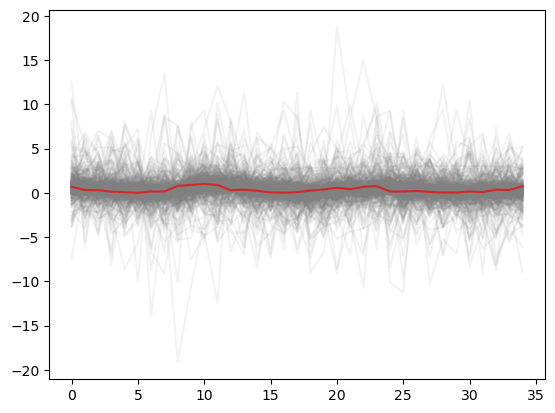
Hello, guys.
I trying to learning PYMC by reimplementing some classical time series models. Now I’m stuck with is the most simple HoltWinters Exponential Smoothing model. It is just an additive and additive damped. In the frequestist implementation we just minimize the SSR of the following function:
def holt_add_dam(double[::1] x, HoltWintersArgs hw_args):
"""
Additive and Additive Damped
Minimization Function
(A,) & (Ad,)
"""
cdef double alpha, beta, phi, betac, alphac
cdef double[::1] err, l, b
cdef const double[::1] y
cdef Py_ssize_t i
err = np.empty(hw_args._n)
alpha, beta, phi, alphac, betac = holt_init(x, hw_args)
y = hw_args._y
l = hw_args._l
b = hw_args._b
err[0] = y[0] - (l[0] + phi * b[0])
for i in range(1, hw_args._n):
l[i] = (alpha * y[i - 1]) + (alphac * (l[i - 1] + phi * b[i - 1]))
b[i] = (beta * (l[i] - l[i - 1])) + (betac * phi * b[i - 1])
err[i] = y[i] - (l[i] + phi * b[i])
return np.asarray(err)
To start I tried to implement the following code.
def step(*args):
y_tm1, l_tm1, b_tm1, α, β, ϕ = args
l = alpha * y_tm1 + (1 - alpha) * (l_tm1 + phi * b_tm1) # update the level
b = beta * (l - l_tm1) + (1 - beta) * phi * b_tm1 # update the trend
μ = l + ϕ * b # forecast
return (l, b, μ), collect_default_updates(inputs=args, outputs=[μ])
with pm.Model() as model:
alpha = pm.Uniform('alpha', 0, 1)
beta = pm.Uniform('beta', 0, 1)
phi = pm.Uniform('phi', 0.8, 0.98)
sigma = pm.HalfNormal('sigma', 0.1) # variance
l0 = pm.Normal('l0', Y[0], 0.1) # initial level
b0 = pm.Normal('b0', 0, 0.1) # initial trend
yend = pm.Normal('yend', Y[-1], 0.1) # end value
# Observed Data
y_obs = pm.MutableData('y_obs', Y)
[l, b, yhat], updates = scan(fn=step,
sequences=[{'input':y_obs, 'taps':[0]}],
outputs_info=[l0, b0, None],
non_sequences=[alpha, beta, phi],
strict=True)
pm.Normal('obs', mu=yhat, sigma=sigma, observed=y_obs)
This takes hour and hours to sample what is some how impossible as the frequestist approach takes seconds or few minutes by gridsearching. So, then I tried to change a little.
def step(*args):
y_tm1, l_tm1, b_tm1, α, β, ϕ, σ = args
l = alpha * y_tm1 + (1 - alpha) * (l_tm1 + phi * b_tm1) # update the level
b = beta * (l - l_tm1) + (1 - beta) * phi * b_tm1 # update the trend
μ = l + ϕ * b # forecast
y = pm.Normal.dist(mu=μ, sigma=σ)
return (l, b, y), collect_default_updates(inputs=args, outputs=[y])
with pm.Model() as model:
alpha = pm.Uniform('alpha', 0, 1)
beta = pm.Uniform('beta', 0, 1)
phi = pm.Uniform('phi', 0.8, 0.98)
sigma = pm.HalfNormal('sigma', 0.1) # variance
l0 = pm.Normal('l0', Y[0], 0.1) # initial level
b0 = pm.Normal('b0', 0, 0.1) # initial trend
# Observed Data
y_obs = pm.MutableData('y_obs', Y)
[l, b, y_hat], updates = scan(fn=step,
sequences=[{'input':y_obs, 'taps':[0]}],
outputs_info=[l0, b0, None],
non_sequences=[alpha, beta, phi, sigma],
strict=True)
obs = model.register_rv(y_hat, name='obs', observed=y_obs)
Again it is taking hours and hours to sample. Both prior predictive look great.
How can I improve the models above? Or even how sould I implement this kind of model?