Hello everyone!
I have recently been working on xarray-einstats, a small library to make working with xarray objects easier. It is very common in Bayesian modeling to need to do further post-processing on the posterior samples in order to get meaningful and interpretable results, in many cases, these operations involve statistical or linear algebra, two areas that xarray is not focused on.
xarray-einstats wraps many functions from numpy.linalg module, from scipy.stats module, from einops and also has a few extras like a numba powered 1D histogram that works on xarray objects and can bin over arbitrary dimensions, parallelizing over the rest of dimensions (used in the rugby notebook too).
Moreover, in addition to its own documentation, which I have tried to make quite exhaustive, you can already see it in action in some pymc-examples notebooks (also updated already to use v4), whose use of xarray-einstats I’ll use to show some of its features.
- A Hierarchical model for Rugby prediction — PyMC documentation
- Factor analysis — PyMC documentation
- Model building and expansion for golf putting — PyMC documentation
In the rubgy notebook for example, we start with a 3d chain, draw, team array whose values are the points each team scored during the competition and convert those to the ranks of each team:
from xarray_einstats.stats import rankdata
pp["rank"] = rankdata(-pp["teamscores"], dims="team", method="min")
Then bin the chain and draw dimensions away, generating 6 histograms in parallel to generate a 2d array with the probabilities of each team finishing in each rank:
from xarray_einstats.numba import histogram
bin_edges = np.arange(7) + 0.5
data_sim = (
histogram(pp["rank"], dims=("chain", "draw"), bins=bin_edges, density=True)
.rename({"bin": "rank"})
.assign_coords(rank=np.arange(6) + 1)
)
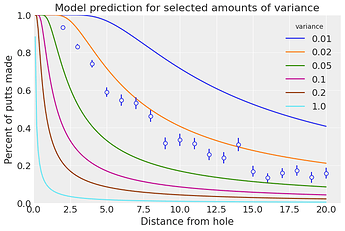
In the golf putting notebook, we define a forward_angle_model with xarray-einstats, then use it indistintively with 1d or 3d inputs for plotting and posterior predictive simulations. In the 1d input for plotting:
def forward_angle_model(variances_of_shot, t):
norm_dist = XrContinuousRV(st.norm, 0, variances_of_shot)
return 2 * norm_dist.cdf(np.arcsin((CUP_RADIUS - BALL_RADIUS) / t)) - 1
_, ax = plt.subplots()
t_ary = np.linspace(CUP_RADIUS - BALL_RADIUS, golf_data.distance.max(), 200)
t = xr.DataArray(t_ary, coords=[("distance", t_ary)])
var_shot_ary = [0.01, 0.02, 0.05, 0.1, 0.2, 1]
var_shot_plot = xr.DataArray(var_shot_ary, coords=[("variance", var_shot_ary)])
# both t and var_shot_plot are 1d DataArrays but with different dimension
# thus, the output is a 2d DataArray with the broadcasted dimensions
forward_angle_model(var_shot_plot, t).plot.line(hue="variance")
plot_golf_data(golf_data, ax=ax) # This generates the scatter+error plot
ax.set_title("Model prediction for selected amounts of variance");
Bonus: I have also been looking into its potential to improve ArviZ using it as that would mean even better ArviZ-xarray integration, aka better scaling to posteriors with hundreds of variables/dimensions and much better scaling to models that don’t fit to memory. You can see some experiments on that and comparisons between xarray-einstats based rhat to the current ArviZ rhat in my GitHub.